6.5 多输入通道和多输出通道

🏷️sec0605_Convolutional_Multichannels

在提到神经网络的卷积时，通常都是指由多个并行卷积组成的运算。通道数是卷积神经网络非常重要的超参数，它对模型性能的影响非常显著。一般来说，通道包括两种类型，一种是输入通道，一种是输出通道。前者由输入特征图本身的属性决定，后者决定了卷积层所生成的特征图的维度。单通道通常无法很好地完成样本特征的提取。一方面，单通道的输入信息量较少，例如灰度图无法提供色彩信息的，而自然界的场景却是总是色彩丰富的。所以，输入通常并非是只是二维的标量，而是由一系列观察数据组合而成高维张量。另一方面，只具有单个卷积核的卷积运算只能从样本中提取到一种类型的模式，即便它被作用到多个不同的空间位置，也只是去获取不同空间位置的同一种特征。而我们通常希望网络在每一层的不同空间位置都能够获取到多种不同类型的特征。

图6-23 彩色图像上的多通道信息

在卷积神经网络中，卷积核的主要作用是在输入特征图中去搜索和识别某种特定的模式，这些模式通常具有局部特性。所以，它们只能反映局部区域的特征，而不是整个样本。举个例子，比如你的最终目标是去识别一只可爱的小兔子。其实，你并不能直接一眼就将它识别出来，而是先去观察它的一些具有特色的细节信息，例如耳朵、眼睛、毛发、轮廓等，通过对这些不同粒度的显著性特征的组合，你才能判断它是一只兔子而不是一只小狗。这个过程和卷积神经网络识别目标的过程非常相似。我们之前介绍过，不同的核心会去识别不同的特征，比如色彩、边缘、纹理等直观的特征，或者是锐化、模糊等属性特征。通过学习，模型可以利用卷积核不同的参数去匹配这些不同的特定模式。在图6-23 中的第一个卷积核，它会去匹配粉红色通道里的一个点，第四个卷积核匹配的是一种从左上往右下延伸的边缘的纹理，左下角的第七个卷积核匹配的是从左下到右上存在紫蓝绿橙的色彩渐变的性质。此时，你可以认为每个卷积核它都能够识别某一种特定的模式，并将样本图中所有的这种模式都给输出出来。在图6-23 的例子中，你可以认为它的输出通道等于9，并且对于每个输出通道，图片进去之后都会产生一个对应模式的特征图。这就是输出通道干的事情。假设将这些输出通道作为输入都丢给下一层，下一层的卷积核就会将这些输入进行一定的组合并获得更抽象的复合特征。整个复合的过程通过加权相加的方式进行。比如，某个输出通道对第一和第四个输入通道比较感兴趣，那么它表达的可能是有粉色信息的左上到右下的边缘纹理；另一个认为第四和第七个输入是比较重要的通道，则它是用来表示带渐变色的边缘纹理。最后，该层包含多少个输出通道就代表了它获得了多少种组合的模式。以上是从层的角度来理解如何利用输入通道和输出通道实现特征的组合，这种机制不仅仅适用于原始像素的输入层，也适用于卷积网络的每一层。对于一个完整的深度神经网络，它可以理解为一种合力的特征提取器。当原始图片以像素的形式被输入到模型中时，开始的一些层会去识别样本中很底层、很局部的信息，比如带角度的边、带颜色的圈等各种不同的纹理，这是底层通道的工作。往上面走，模型就会不断地把局部信息组合起来，形成相对抽象的特征，例如兔子耳朵的绒毛、眼球等部件的关键组成。继续再往上走，各种局部特征经过组合、组合、再组合，到某一层的通道可能就是兔子的身体部件了，比如兔子的耳朵、鼻子或者小脚。这些部件所包含的东西越往上会越丰富，所有的特征组合之后，就变成一只完整的兔子或者是兔子的语义。这就是我们希望深度模型做的事情，或者说模型各个输入和输出通道做的事情。

在多层卷积神经网络中，每一层的输入都是上一层的输出，并且在每个像素位置也都包含多个不同卷积核的输出。在处理图像数据时，我们会把卷积的输入和输出看作是一个三维张量，其形态为[C,H,W]，其中第一个索引用来标明不同的输入通道（channel），例如红、绿、蓝三个色彩亮度，第二和第三个索引用来标明每个通道上的空间位置（height，width）。多通道不仅仅来源于图片的输入层，任何一个中间层相对于后面的层来说，都可以被当作是多通道输入，同时也可以被认为是前面层的多通道输出。此外，大多数深度学习工具包都基于批处理方式进行数据读取，因此通常会使用四维张量来表示数据。新增加的维度用来标明批处理（batch）中不同的实例。常见的数据张量形态包括[N,C,H,W]和[N,H,W,C]。为了简明起见，除非特殊说明，本小节后面的内容将忽略批处理索引。

NCHW通道和NHWC通道的区别

NCHW通道，又称为 channels_first，是nVidia cuDNN库原生支持的数据通道模式。在GPU中进行运算时，NCHW模式比NHWC模式快2.5倍左右。
NHWC通道，又称为 channels_last，是SSE、AVX等CPU指令集比较适合的数据通道模式，它在这些指令集中得到了优化。CPU会沿着最后一个维度C进行计算，在CPU中速度比NCHW更快。
尽管两者存储的数据是相同的，但由于不同的顺序会导致数据访问特性的差异，因此即使执行相同的计算也会带来性能的差异。对于NCHW来说，设备需要把所有通道的数据都读取完毕才能进行计算，因此需要更多的计算存储空间。借助于GPU显存的高带宽和并行性强的特点，其访问内存和计算的控制逻辑相对简单，一次性可以同时计算多个空间位置的像素，所以总体运算速度较快。对于NHWC来说，每次只需要读取三个像素即可完成彩色像素的计算，因此比较适合频率更高的CPU，但由于内存带宽较小，每次只能计算一个像素位置，所以总体运算速度相比GPU的运算要慢一些。
在进行神经网络模型训练的时候，如果使用GPU，建议使用NCHW格式；而在使用CPU进行推理时，推荐使用NHWC格式。此外，OpenCV库在设计时是基于CPU的，所以默认格式为NHWC。TensorFlow等库默认的格式也是NHWC，但它同样支持cuDNN的NCHW。

6.5.1 灰度图像上使用单卷积核

在介绍多通道卷积前，我们先来看看在灰度图上是怎么使用单个卷积核进行特征提取的。我们知道，灰度图是最简单的图像，它只使用一个颜色通道来对图像进行描述，著名的MNIST数据集中的图像就是灰度图。对于灰度图中的一个像素，最常见的值是[0,1]，其中0表示黑色，1表示白色，0到1之间的浮点值则表示某一个灰度值；在另外一种常见的色谱中，像素的取值范围为[0,255]，相应的0还是表示黑色，255表示白色，0到255之间的浮点值表示某一个灰度值。这两种色彩空间的值是可以进行一对一转换的。简单的说，灰度图就是只有一个灰度值通道的图片。对于类似手写数字这样的目标，灰度图是足够的，并且所有的彩色图片都能够被转换成灰度图。但仍然需要应注意的是，在复杂的场景和任务下仅仅灰度图是无法很好完成工作的。

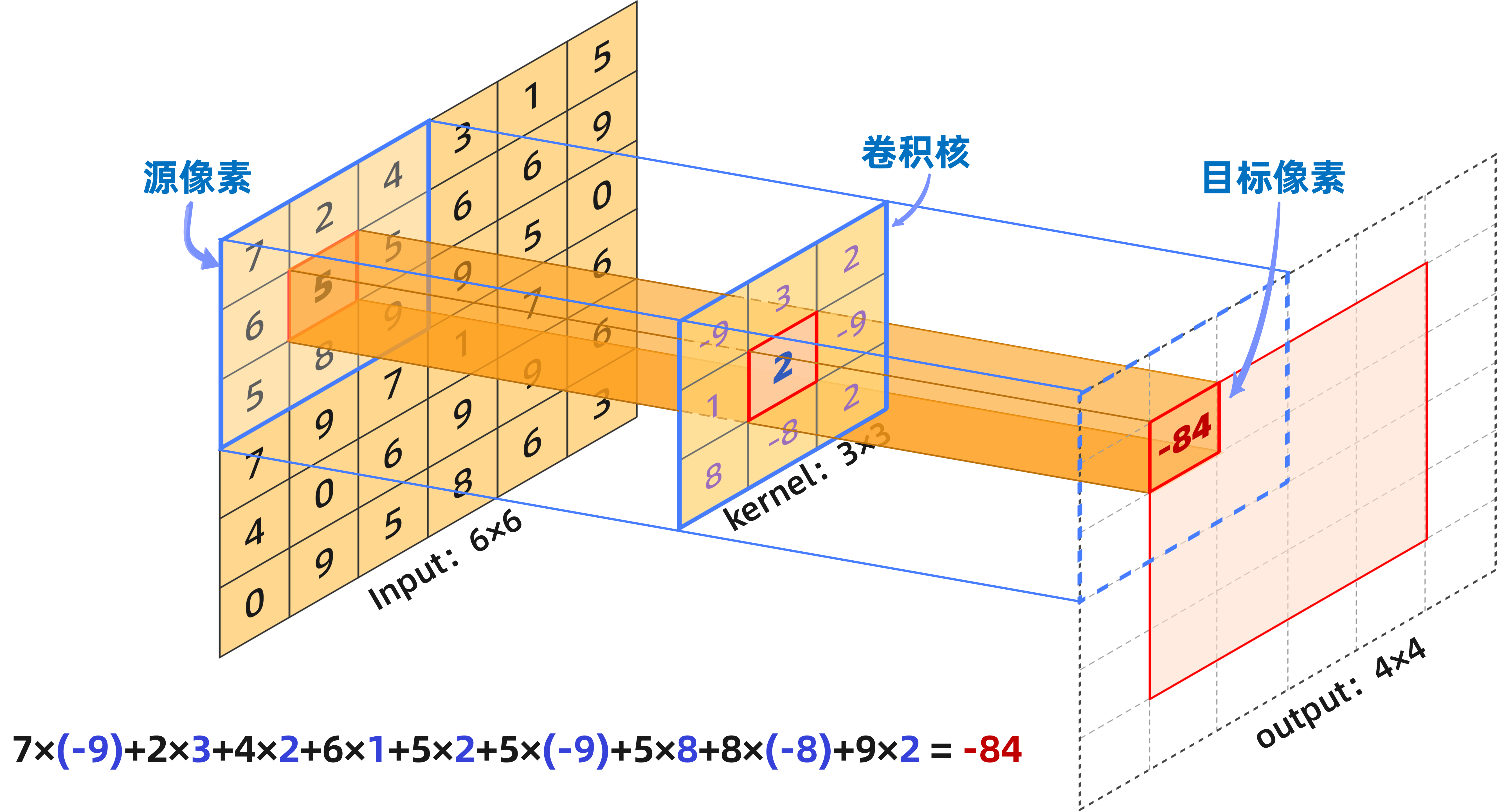
图6-24 在灰度图上使用单个卷积核进行卷积运算

在图像的卷积运算中，卷积最终的结果会按照计算的空间和时间的先后进行顺序排列。每个感知域范围内的卷积计算结果会被映射到下一层对应感知域区域的中间位置。图6-24 给出了一个例子。给定一个 $6×6$ 的输入和一个 $3×3$ 的卷积核。第一个卷积计算的位置位于输入图左上角开始的 $3×3$ 的区域。不难计算，其结果等于 $-84$ 。如果下一个卷积层也存在一个 $6×6$ 的矩阵，那么刚刚计算获得的值将被赋予到第二行、第二列的位置，对应回去就是输入的正中间。换句话说，在图像中卷积计算的值会被赋予到结果矩阵的正中心。再之后，只需要按照从左到右、从上至下进行Z字形滑动并计算输出，就可以生成完整的卷积特征图了。在该图中，由于输出是位于 $3×3$ 矩阵的正中心，且只是一个标量，所以会使得输出特征图在四周都减少1个像素。最终会导致完整的输出特征图的四周都减少1个像素，变成 $4×4$ 。所以如果需要保证输出的尺度不变，我们就必须在输入的四周各增加一个像素的零填充。以上就是单输入、单特征的卷积运算，或者说是在灰度图上只提取了一种特征的情况。

为了便于理解，我们使用下面的代码实现图6-24 卷积的完整运算。首先导入必要的库和自定义类common，该类保存了我们在第 6.3 小节中定义的互相关计算函数。

import numpy as np
import sys
sys.path.append(r'D:\WorkSpace\DeepLearning\WebsiteV2')   # 定义自定义模块保存位置
from codes.paddle import common
import paddle

接下来，我们定义一个单输入通道、单输出通道的卷积计算函数，它直接返回两个二维张量进行互相关运算的结果。

程序清单6-13 定义单输入单输出卷积函数

# codes06013_conv2d_in_single_out_single
def conv2d_in_single_out_single(X, K):
    # 对输入和卷积核执行互相关运算，并直接返回运算结果
    return common.cross_correlation(X, K)

最后，我们构造与图6-24 相同的输入张量 $X$ 和核张量 $K$ ，以验证灰度图上使用单个卷积核进行互相关运算的输出。

程序清单6-14 输出单输入单输出的卷积运算结果

# codes06014_print_conv2d_in_single_out_single
# 1.定义输入张量和核张量（输入：6×6，卷积核：3×3）
X = paddle.to_tensor([[7,2,4,3,1,5],[6,5,5,6,6,9],[5,8,9,9,5,0],[7,9,7,1,7,6],[4,0,6,9,9,6],[0,9,5,8,6,3]], dtype='float32')
W = paddle.to_tensor([[-9,3,2],[1,2,-9],[8,-8,2]], dtype='float32')
# 2.计算多输入单输出的运算结果
print(conv2d_in_single_out_single(X, W))

Tensor(shape=[4, 4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[-84. , -29. , -52. , -45. ],
        [-91. , -55. ,  29. , -35. ],
        [ 3.  , -43. , -104., -93. ],
        [-134., -79. , -115.,  19. ]])

从以上结果可以看到，使用一个卷积核对输入进行特征提取只能生成深度维度为 $1$ 的特征矩阵。

6.5.2 RGB图像上使用单卷积核

在灰度图中，由于输入的通道数为 $1$ ，所以我们所构造的卷积核的深度也为 $1$ 。此时，隐含了一个基础的条件，那就是卷积核的输入通道数和输入数据的输入通道数是相同的。所以，当输入包含多个通道时，我们就需要构造一个与输入数据具有相同输入通道的多层卷积核，以便与输入数据能够正常执行互相关运算。假设输入通道数为 $c_i$ ，无论输入是图像还是某个隐层，都应该存在该层的卷积核的输入通道数也为 $c_i$ 。如果卷积核的窗口大小为 $k_h × k_w$ ，那么当 $c_i=1$ 时，卷积核可以被看作是一个 $k_h × k_w$ 的二维张量，也即上一小节中灰度图上使用单卷积核的情况。当 $c_i=3$ 时，卷积核可以被看作是一个 $k_h×k_w×3$ 的张量，此时就相当于在RGB图像上使用一个三维张量核进行特征提取。当 $c_i$ 等于任意大于 $3$ 的值时，卷积核就是任意卷积层上的一个三维张量核。按照我们在第 6.3.7 小节中的讨论，此时的 $c_i$ 既是该卷积层的特征图的深度维度，同时也是该卷积层上卷积核的深度维度。

图6-25 在RGB图像上使用单卷积核进行互相关运算

为了便于理解，下面我们还是以输入图为例，但应知道下面的讨论适用于任何一个卷积层。假设存在一幅尺度为 $6×6$ 的彩色的输入图，此时输入通道数 $c_i=3$ 。假设忽略批量通道 $N$ ，则输入张量可以表示为 $6×6×3$ 或 $3×6×6$ 。

图6-25 给出了该输入张量，对于输入张量中的三个通道（红色、蓝色、绿色），我们需要给它们分别赋予一个相同维度的卷积核，比如图中的浅红色、浅绿色和浅蓝色矩阵。也就是刚刚提到的卷积核输入通道数应该与输入数据的输入通道数一致。对于这三个二维卷积核，它们都有自己独立的值，且通常不相同。也就是说，第一个二维卷积核针对输入中的第一个矩阵做卷积，第二个二维卷积核针对输入中的第二个矩阵做卷积，依此类推。如果我们将这三个二维卷积核看成是一个深度为 $3$ 的整体，那么这三个二维卷积核就变成了一个三维的卷积核。对于这个三维的卷积核，我们可以认为它就是一个卷积核，只不过它的深度不再是 $1$ ，而是 $3$ 。接下来的问题就是如何获得输出张量。具体来看，比如第一个输出值 $-21$ 是如何计算出来的。如图所示，它是卷积核与输入起始区域像素的互相关运算的结果，即 红色矩阵*浅红色矩阵+绿色矩阵*浅绿色矩阵+蓝色矩阵*浅蓝色矩阵 = -21。简单的说，卷积核与其对应的每层的局部区域做卷积操作，最后再进行累加，就可以得到对应位置的输出值。如果将卷积核按照从左至右，从上至下的顺序进行滑动，并使用相同的方法进行互相关运算，就可以得到整个卷积层最终的输出值。值得注意的是，与单通道卷积类似，此时的输出张量依然是一个二维矩阵，因为每次卷积运算的结果依然只是一个标量。与单通道卷积不同的是，多输入通道卷积融合的是所有通道的点积计算结果，而不仅仅只是一个二维矩阵的点积。将以上过程公式化后可以得到输出：

$Y = \sum^{c_i}_{i=0} X_{i,:,:} * W_{i,:,:} + b_i \tag{6.15}$

其中，输入 $X$ 和卷积核 $W$ 都是三维张量。下标 $c_i$ 表示输入通道的数量， $c$ 是通道数channel， $i$ 代表输入input。输入 $X$ 的尺度为 $c_i×n_h×n_w$ ，其中 $n_h×n_w$ 是输入图片的分辨率。卷积核 $W$ 的尺度为 $c_i×k_h×k_w$ ， $k_h$ 和 $k_w$ 分别表示卷积核的高度和宽度。此外，对于每个输入通道 $c_i$ 都有一个偏置 $b_i$ ，所以偏置是一个长度为 $c_i$ 的向量。偏置只略微改变输出值的大小，并不会影响输出的维度。由于输入和卷积核都有 $c_i$ 个通道，我们可以对每个通道输入的二维张量和卷积核的二维张量进行互相关运算，再加上偏置，最后再对通道 $c_i$ 进行求和得到二维张量。最终的输出 $Y$ 是一个 $n_h×n_w$ 的二维张量。也就是说，它是一个单通道的输出，因为不管你的输入是多少个通道，最终都会将它的结果进行累加，所以最后总是会变成一个通道。这就是卷积层的多通道输入。

为了加深理解，下面的代码实现了多输入通道的互相关运算。它的基本思想是先对每个输入通道都单独做二维互相关运算，然后将各层的运算结果进行累加，此处忽略偏置。

程序清单6-15 定义多输入单输出卷积函数

# codes06015_conv2d_in_multi_out_single
def conv2d_in_multi_out_single(X, K):
    # 按通道遍历计算每一层的互相关运算结果，然后再按通道进行累加
    return np.sum(common.cross_correlation(x, k) for x, k in zip(X, K))

下面我们构造与图6-25 相同的输入张量 $X$ 和核张量 $K$ ，以验证互相关运算的输出。

程序清单6-16 输出多输入单输出的卷积运算结果

# codes06016_print_conv2d_in_multi_out_single
# 1.定义输入张量和核张量（输入：3×6×6，卷积核：3×3×3）
X = paddle.to_tensor([[[7,2,4,3,1,5],[6,5,5,6,6,9],[5,8,9,9,5,0],[7,9,7,1,7,6],[4,0,6,9,9,6],[0,9,5,8,6,3]],
            [[1,3,1,7,2,4],[3,1,0,5,3,4],[8,4,8,2,5,7],[5,1,2,5,7,6],[9,1,1,7,3,2],[7,9,4,9,4,0]],
            [[3,3,3,8,6,6],[2,8,0,4,9,0],[1,3,7,8,3,3],[7,9,3,8,6,9],[2,5,1,8,7,5],[2,3,0,8,8,1]]], dtype='float32')
W = paddle.to_tensor([[[-9,3,2],[1,2,-9],[8,-8,2]],
            [[1,-2,1],[2,3,-6],[-7,6,2]],
            [[3,9,2],[-1,7,4],[2,6,-6]]], dtype='float32')
# 2.计算多输入单输出的运算结果
print(conv2d_in_multi_out_single(X, W))

Tensor(shape=[4, 4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[-21.,  35., 101., 152.],
        [ 41.,  84., 177.,  80.],
        [ 97.,  38., 107.,  29.],
        [ 66., -73.,  99., 203.]])

可以看到，多通道输入卷积计算的结果也是一个深度为 $1$ 的特征矩阵，不过它的每个元素都是各层互相关运算的累加值。

6.5.3 RGB图像上使用多卷积核

到目前为止，不管你有多少个输入通道，我们都只能得到一个单通道的输出。也就是说，你输入的如果是RGB的三原色通道，最终你得到的依然是一个单通道的特征图。在所有流行的神经网络架构中，随着网络层次的加深，通常都会在减少特征图空间分辨率的同时增加输出通道的维数。因为，每个通道都可以被看作是一种不同的特征响应。也就是说，如果现在我想要我的输出也是多通道输出。那么，我只需要去设计多组不同的三维卷积核，然后用这些卷积核都去对原来的输入通道进行卷积操作。这些三维卷积核都会为自己生成一个独立的输出通道，我们只需要将这些输出通道一个一个地叠加起来，就能得到一个多输出通道的结果了。此时的输出是一个包含了多个通道，每个通道都是一个二维矩阵的张量。换句话说，多通道输出其实就是一个三维张量。实际应用的情况会更复杂一些，因为每个通道虽然是独立的，但是它们并不是去独立地学习，而是共同使用优化算法来进行学习。所以，多输出通道并不仅仅是学习多个单通道的检测器，它体现的是一种复合学习的机制。

图6-26 在RGB图像上使用多卷积核

令 $c_i$ 依然表示输入通道的数量，同时增加一个参数 $c_o$ 来表示输出通道的数量，并让 $k_h$ 和 $k_w$ 表示卷积核的高度和宽度。为了获得多个通道的输出，对于输入 $c_i×n_h×n_w$ ，我们可以为每个输出通道都创建一个形状为 $c_i×k_h×k_w$ 的卷积核张量。由此，可以得到一个四维的卷积核 $c_o×c_i×k_h×k_w$ 。在互相关运算中，每个输出通道首先按照前面多输入、单输出的规则进行互相关运算，最后再将所有通道的计算结果并联起来。输出 $Y$ 可以表示为：
$Y_{j,:,:,:} = X*W_{j,:,:,:}+b_{j,:},c_i, j=1,2,...,c_o \tag{6.16}$

如上所示，如果完整的输入 $X$ 与第 $j$ 个卷积核 $W_{j,:,:,:}$ 进行互相关运算，将生成第 $j$ 个输出。由于生成每个输出通道张量的输入张量和核张量都具有相同的尺度，所以如果第 $j$ 个输出通道的尺度为 $m_h×m_w$ ，那么最终的输出 $Y$ 的维度就等于 $c_o×m_h×m_w$ 。在这里，输入和输出的通道的数 $c_i$ 和 $c_o$ 是可以进行任意指定的，因为即便所有参数是同时进行优化学习的，输入和输出通道的数量之间也没有太多的相关性。

下面，我们实现一个计算多通道互相关输出的函数，并验证图6-26 的范例。该函数按照输出通道 $c_o$ 的顺序，对每一个卷积核 $j$ 进行迭代，使其与完整的输入 $X$ 进行互相关运算，并在最后将这些输出进行组合，生成一个 $c_o×m_h×m_w$ 的输出张量。

程序清单6-17 定义多输入多输出卷积函数

# codes06017_conv2d_multi_in_multi_out
def conv2d_in_multi_out_multi(X, K):
    # 迭代卷积核的输出通道 c_o，每次都与输入X进行互相关运算，并在最后进行组合，生成c_o维张量
    return np.stack([conv2d_in_multi_out_single(X, k) for k in K], 0)

下面的代码构造了一组与图6-25 相同的输入张量 $X$ 和核张量 $K$ ，用来验证多输出通道的互相关运算。在多输入、多输出通道的环境中，输出包含3个通道，其中第一个通道的结果与代码 codes06014 的输出结果是相同的，因为它们使用的是相同的卷积核。

程序清单6-18 输出多输入多输出的卷积运算结果

# codes06018_print_conv2d_in_multi_out_multi
# 1.定义输入张量和核张量（输入：3×6×6，卷积核：3×3×3×3）
X = paddle.to_tensor([[[7,2,4,3,1,5],[6,5,5,6,6,9],[5,8,9,9,5,0],[7,9,7,1,7,6],[4,0,6,9,9,6],[0,9,5,8,6,3]],
            [[1,3,1,7,2,4],[3,1,0,5,3,4],[8,4,8,2,5,7],[5,1,2,5,7,6],[9,1,1,7,3,2],[7,9,4,9,4,0]],
            [[3,3,3,8,6,6],[2,8,0,4,9,0],[1,3,7,8,3,3],[7,9,3,8,6,9],[2,5,1,8,7,5],[2,3,0,8,8,1]]], dtype='float32')
W = paddle.to_tensor([[[[-9,3,2],[1,2,-9],[8,-8,2]],
            [[1,-2,1],[2,3,-6],[-7,6,2]],
            [[3,9,2],[-1,7,4],[2,6,-6]]],
            [[[3,-2,2],[-1,2,7],[-5,-3,2]],
            [[1,4,-1],[2,-3,5],[4,-6,3]],
            [[3,-8,2],[-2,1,4],[-1,2,2]]],
            [[[1,-2,2],[-1,2,-4],[-4,-3,4]],
            [[1,3,-2],[2,-2,5],[3,5,1]],
            [[2,-6,4],[3,-2,4],[-1,-2,-2]]]], dtype='float32')
# 2.计算多输入单输出的运算结果
print(conv2d_in_multi_out_multi(X, W))

[[[-21.  35. 101. 152.]
  [ 41.  84. 177.  80.]
  [ 97.  38. 107.  29.]
  [ 66. -73.  99. 203.]]

 [[ 94.  31.  69.  50.]
  [103. 101. 103.   5.]
  [145. 109.  48. 110.]
  [ 15. 178.  79.  69.]]

 [[ 20.  58. -17. -25.]
  [-20. -33.  73.  49.]
  [ 66. 115.  -9.  42.]
  [ 27. 100.   7.  45.]]]

从以上结果看，在使用多个卷积核对输入进行特征提取时，最终的输出张量的深度维度为卷积核的个数是相同，也就是我们前面介绍的卷积核的个数决定了输出通道的数量。

6.5.4 1×1卷积

在卷积神经网络中，还存在一种非常特殊的卷积层，那就是 $1×1$ 卷积。简单地说， $1×1$ 卷积就是使用高和宽都等于 $1$ 的卷积核去对特征图进行互相关运算。这意味着，它不会去识别特征图的空间信息，因为它每次只看一个像素，无法看到像素的周围区域。所以，它不会去识别这个通道中的空间模式是什么。这种卷积看上去似乎没有多大的意义，毕竟卷积的本质是有效提取相邻像素间的上下文关系，而 $1×1$ 卷积显然不具备这种功能。尽管如此， $1×1$ 卷积依然是十分流行的应用，被融合到许多复杂的深层网络中。那么它究竟是用来做什么呢？简单的说，它就是在做不同通道信息的融合。

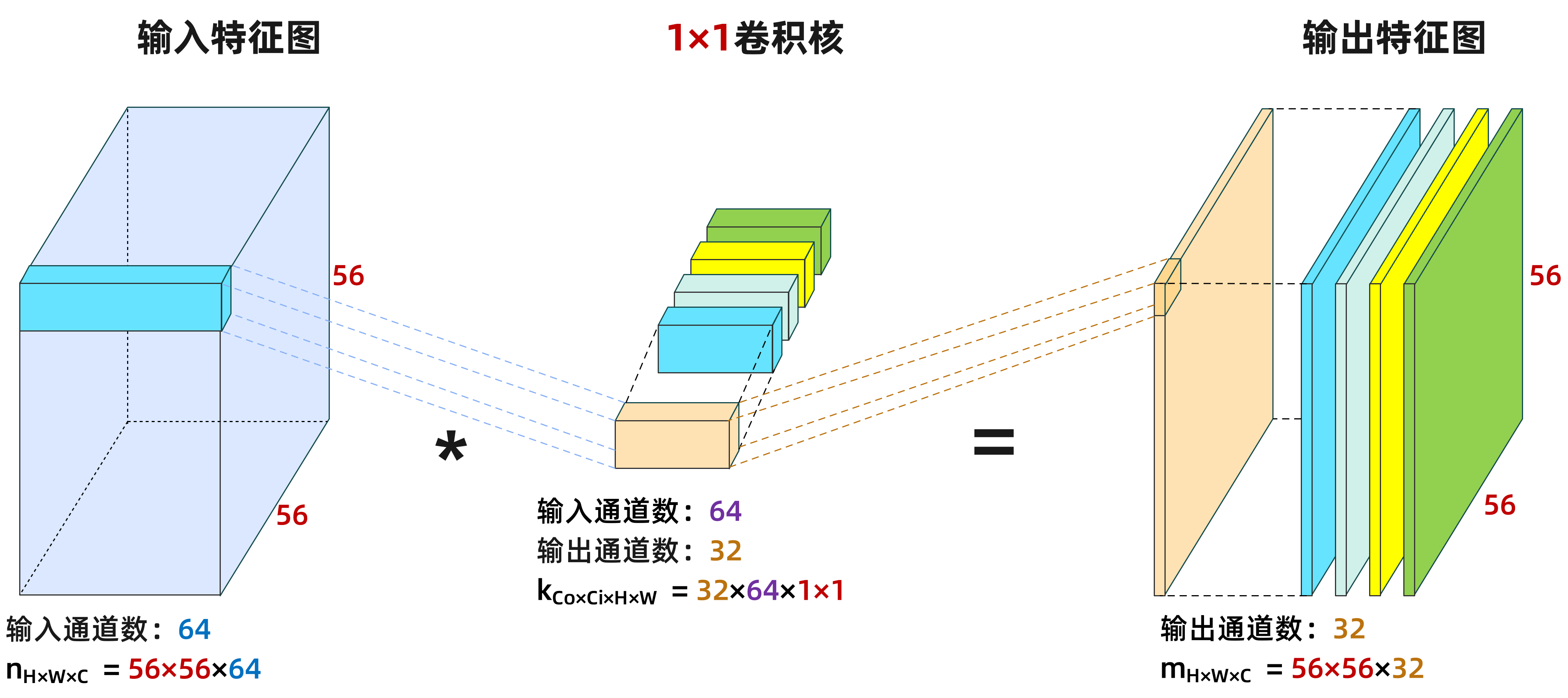
图6-27 1×1卷积原理图

由于 $1×1$ 卷积的窗口只有一个像素，因此它失去了卷积层原有的基本能力，即在相邻元素间获取上下文信息，它的计算只发生在通道维度上。图6-27 展示了使用32个 $1×1$ 卷积核与64个输入通道的输入之间的互相关计算。对于输入 $X$ ，它包含64个输入通道，并且其高度和宽度都是56个像素。在输入特征中，深蓝色立方体是索引为0的像素，它的深度是64，但高度和宽度都是1个像素。它与第一个浅黄色的 $1×1$ 卷积核进行卷积运算后，将在输出特征图中生成位置索引为0的一个深度为1的像素。当这个浅黄色卷积核完成对整个 $56×56$ 的输入的扫描后，它将生成一个 $56×56×1$ 的特征图。这是第一个 $1×1$ 卷积核所生成的特征图，它将深度为64的输入融合成了深度为1的输出，但特征图的高度和宽度保持不变，依然是 $56×56$ 。如果存在32个这样的 $1×1$ 卷积核，并且都按照第一个卷积核相同的方式去扫描输入特征图，最终将得到一个 $56×56×32$ 的输出特征图。在这个输出中，每个 $1×1$ 的卷积核都会唯一地对应1个 $56×56$ 的特征矩阵。将这32个二维特征矩阵组合在一起就能构成一个深度为32的输出张量。在这个过程中，输入特征图和输出特征图的尺度是相同的，并且在卷积生成的过程中，每个像素通道都没有和周围的像素进行信息交换。这意味着，输出特征图中的每个像素与输入特征图中的每个像素，在二维空间位置上是一一对应的。所以， $1×1$ 卷积只做了通道的融合，并没有进行空间模式的识别和变换。如果你愿意，你可以增加或减少 $1×1$ 卷积核的数量，从而实现输出特征图深度的增加或减少。这听起来是一件很酷的事，因为我们一般认为，从特征图深度的维度来看，每个层次都代表着一种特定的模式。所以，我们可以通过 $1×1$ 卷积来实现对复杂数据的维度增加，从而获取更多种类的模式信息；也可以通过 $1×1$ 卷积实现对简单数据的降维，从而实现模型参数的减少，进而降低模型的计算复杂性。 $1×1$ 卷积还有另外一个重要的说法。由于它不做空间匹配，其输入和输出具有相同的分辨率，所以输出中的每个元素都是输入图像中同一个二维空间位置中不同层的元素的线性组合。我们可以将 $1×1$ 卷积看作是在每个像素位置应用的全连接层，以 $c_i$ 个输入值转换成 $c_o$ 个输出值。由于 $1×1$ 卷积依然是卷积，所以它也遵循参数共享的特性，因此跨像素的卷积核的权重也是相同的。所以， $1×1$ 卷积的参数维度就等于 $c_o×c_i×1×1$ = $c_o×c_i$ ，再额外加上一个偏置。反过来，为了构建全卷积网络，我们也可以将全连接层转换为 $1×1$ 卷积，这种方法在后面的模型中会经常被用到。2021年出了一篇很吸引人的论文 MLP-Mixer（Tolstikhin, 2021），作者Tolstikhin说他们的MLP能够打败卷积神经网络，实际上他们就是用了大量的 $1×1$ 卷积。从某种角度上来说，MLP-Mixer确实是全连接层，但也可以说其也是卷积层。

下面，我们使用全连接层来实现 $1×1$ 卷积。注意在进行矩阵乘法前需要将四维的输入张量和权重张量调整为二维矩阵，也即将卷积运算转换为全连接网络的矩阵乘法，表示为：
$Y_{c_o×(h×w)} = K_{c_o, c_i}×X_{c_i, h×w} \tag{6.17}$

程序清单6-19 定义1×1卷积函数

# codes06019_conv2d_in_multi_out_1x1
def conv2d_in_multi_out_1x1(X, K):
    c_i, h, w = X.shape
    c_o = K.shape[0]
    X = X.reshape((c_i, h * w))
    K = K.reshape((c_o, c_i))
    # 全连接层中的矩阵乘法
    Y = paddle.matmul(K, X)
    return Y.reshape((c_o, h, w)).numpy()

下面我们构造一个输入张量 $X$ 和一个包含32个输出通道的 $1×1$ 卷积核。然后分别使用全连接形式和多通道卷积形式计算它们之间的相关关系。最终的输出是验证两种模式的计算能否得到相同的输出。

程序清单6-20 输出1×1卷积运算结果

# codes06020_print_conv2d_in_multi_out_1x1
# 1.定义输入张量和核张量
X = paddle.to_tensor([[[1,1,1,0,0],[0,1,1,1,0],[0,0,1,1,1],[0,0,1,1,0],[0,1,1,0,0]],
            [[1,0,1,1,0],[0,1,1,1,1],[0,0,1,1,1],[0,0,1,1,0],[0,1,1,0,1]],
            [[1,1,1,1,0],[0,1,1,1,0],[0,0,1,1,1],[0,0,1,1,0],[0,1,1,0,0]]], dtype='float32')
W = paddle.rand([32,3,1,1])
# 2.计算多输入单输出的运算结果
Y1 = conv2d_in_multi_out_1x1(X, W)
Y2 = conv2d_in_multi_out_multi(X, W)
print('Y1与Y2的关系是：{}。\n 其形态为：{}。'.format('完全相同' if (Y1==Y2).any() else '不相同', Y2.shape))

Y1与Y2的关系是：完全相同。
 其形态为：(32, 5, 5)。

从以上结果看， $1×1$ 卷积也是一种多输入、多输出卷积，并且它的输出结果等价于全连接层的矩阵乘法。

6.5.5 小结

多通道输入和多通道输出是拓展卷积层模型最有效的方法之一，在卷积网络中它们都可以被认为是一种超参数，由用户任意指定获得。
输入通道的设置通常不需要专门指定，对于一般的卷积层它的值由上一层卷积核的数量决定，对于第一个卷积层它的值由样本的维度决定。
在卷积网络中，每个输入通道都对应一个二维的卷积核，所有二维卷积核组合起来就是一个三维卷积核。每个三维卷积核都能输出一个二维特征图，我们称之为一个输出通道。
每个卷积层都可以包含多个三维卷积核，并且每个独立的三维卷积核都可以产生一个输出通道，一个输出通道对应于一种特定的模式或特征。当存在多个卷积核时，最终可以产生多个输出通道，组合起来就是最终的三维输出特征图。

6.5.5 练习

假设某网络只有一个卷积层，并且输入图像分辨率为 $c_i×n_h×h_w$ ，卷积核的尺度为 $c_o×c_i×k_h×k_w$ ，填充和步幅分别为 $(p_h, p_w), (s_h, s_w)$ 。试计算：
1). 前向传输的时间复杂度
2). 该网络的的内存占用量
假设将输入通道数 $c_i$ 和输出通道数 $c_o$ 分别增加1倍，则最终的计算时间复杂度会（）。
A. 保持不变
B. 变为原来的2倍
C. 变为原来的4倍
D. 变为原来的8倍
假设存在两个卷积核 $k_1$ 和 $k_2$ ，若不存在非线性激活函数，是否可以使用单个卷积核来实现这两个卷积核的功能？
A. 可以
B. 不可以
由于灰度图像只有一个颜色通道，因此在使用卷积神经网络对灰度图进行特征提取和建模时，只能使用一个卷积核。
A. 对
B. 错
试计算如下特征图和卷积核的计算结果。

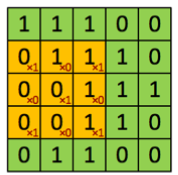
A. 2
B. [[0,0,1],[0,0,0],[0,0,1]]
C. 1
D. [[0,1,1],[0,0,1],[0,0,1]]
若对一个分辨率为100×100的RGB图像使用卷积神经网络（卷积核的高宽为3×3）进行特征提取，则第一个卷积层的卷积核的个数是多少？
A. 9
B. 10000
C. 3
D. 无法确定
假设存在一个5×5×4的特征图，如果我们使用一个3×3×4的卷积核对这个特征图进行特征提取（假设填充为0和步幅为1），则最终将得到的特征图形态为（）。
A. 3×3×4
B. 3×3×1
C. 5×5×4
D. 5×5×1