2.2 神经网络的引擎:微积分
🏷sec0202_Mathematics_Calculus
公元前500多年,古希腊人把多边形分解成多个三角形,实现了多边形面积的求解。公元前200多年,阿基米德使用内、外切多边形结合的穷竭法来计算圆周率 ,最终他使用96边形获得了3.1428~3.1429的推断。400多年后,中国魏晋时期的伟大数学家刘徽打破了这个纪录,他仅仅使用基于内接多边形的割圆术就将圆周率精确到了小数点后的第4位3.1416。又过了200多年,南北朝著名数学家祖冲之利用割圆术在12288条边的多边形上得到了圆周率更新精准的记录3.1415926~3.1415927,这一记录一直保持了一千多年。图2.2.1 和 程序清单2.2.1 给出了基于割圆术的内接多边形圆周率计算方法。

图2.2.1 刘徽割圆术示意图
我们不妨假设从一个边长为1的正六边形开始进行割圆术的计算,此时它的边长刚好等于圆的半径。每次进一步割圆都将边长的数量增加一倍,最终将获得一个正2n边形。从上图可以直观看出,随着多边形边数量的增长,多边形的周长也越来越接近于圆的周长。设第n-1代内切多边形(以正六边形为例)的边长为,利用勾股定理,我们可以得到小三角形ACB的高h的表达式:
进一步,我们可以获得第n代多边形的边长 ,即:
此时,第n代多边形的边数为 。如果我们使用第n代多边形的周长作为圆的周长,那么,我们就可以通过圆面积的计算公式获得圆周率:
下面是割圆术的Python实现。
# codes02028_CyclotomicMethod # 1. 设初始形状为六边形,且半径r=OA=OC=1,根据勾股定理不难计算第一次割圆后的边长AC # 2. 根据圆的周长公式C=PI*d,可以得到PI=C/d=C/2r # 3. 使用隔圆术迭代地生成2n条边的多边形,当边数逐渐增加时,多边形的周长也逐渐接近圆的周长C import math def LiuHui(n): # 设当前边长为x,根据勾股定理计算割后边长 def f(x): r = 1 h = r - math.sqrt(r**2-(x/2)**2) # 计算高BC return math.sqrt(h**2 + (x/2)**2) # 返回割后边长 x = 1 # 设初始边长=圆的半径=1 k = 6 # 设初始边数为6 for i in range(n): x = f(x) # 获取割后边长 k = k * 2 # 获取边数,每次循环后边数翻倍 PI = x * k / 2 print('{}边形的近似圆周率:{}'.format(k, PI)) return if __name__ == '__main__': print('参考圆周率:{}'.format(math.pi)) n = 11 LiuHui(11)
参考圆周率:3.141592653589793 12边形的近似圆周率: 3.105828541230249 24边形的近似圆周率: 3.1326286132812378 48边形的近似圆周率: 3.1393502030468667 96边形的近似圆周率: 3.14103195089051 192边形的近似圆周率: 3.1414524722854624 384边形的近似圆周率: 3.141557607911858 768边形的近似圆周率: 3.1415838921483186 1536边形的近似圆周率: 3.1415904632280505 3072边形的近似圆周率: 3.1415921059992717 6144边形的近似圆周率: 3.1415925166921577 12288边形的近似圆周率:3.141592619365384
上面的代码给出了使用割圆术求取圆周率的过程。不难发现,随着圆的内接正多边形边数的增加,圆周率也越来越接近真实的参考圆周率,当多边形增长到12288边时,我们获得了与数学家祖冲之相同的近似圆周率3.1415926。正如刘徽在《九章算术》 (Liuhui, 200) 中对割圆术的形容 “割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣。”,这种通过不断迭代优化求圆周率的方法,我们称之为 逼近法(method of exhaustion)。事实上,逼近法就是 积分(Integration) 的起源。
另一方面,人们对于无穷、极限以及无穷分割等概念的认知早在希腊时期就开始萌生。例如,公元前五世纪,希腊哲学家德谟克利特提出原子论,他认为宇宙万物是由极细的原子构成。在中国的先秦时期,《庄子.天下篇》中也提到“一尺之捶,日取其半,万世不竭”,这也是指无穷分割。一般来说,我们将类似关于极限、导数、无穷划分的概念称为 微分(Differentiation)。在微分学中,最重要的应用是优化问题,即如何使模型的输出尽力而为地与真实目标一致。 例如 2.1.6 小节中所提到的使用范数来计算两个对象之间的相似度,以及最小化预测值和真实观察值之间的距离等。
在深度学习中,我们训练模型的过程实际上也是一个不断优化模型参数的过程。训练致力于让模型通过看到越来越多的数据后变得越来越好。一般来说,优化过程意味着最小化一个 损失函数(loss function),这个函数的值称为损失值,是一个被用来衡量模型有多糟糕这个问题的分数。我们的最终目标就是尽力而为地使损失值变为0,当然这个目标通常是无法实现的,优化的目的就是使结果变得越来越好。所以,深度学习真正关心的是如何通过训练生成一个在那些从未见过的数据上表现良好的模型。
在整个训练过程中,模型只能根据实际看到的数据(训练数据)进行拟合,而不能在那些未见过的数据(测试数据)上进行学习。模型拟合通常由两个关键任务构成,分别是 优化(optimization) 和 泛化(generalization)。优化是指模型拟合训练数据的过程,泛化则是指在数学原理和智慧者的指导下,通过训练所获得的模型能够帮助我们对那些超出训练数据的数据也具备有效的分析与判断能力。
关于优化问题,常见的求解方法有梯度下降法、牛顿法、拟牛顿法、共轭梯度法、拉格朗日乘数法、KKT条件法以及一些启发式的优化算法,例如遗传算法、模拟退火算法等。为了帮助读者更好地理解这些优化算法的求解方法,本小节将简要介绍一些关于导数、梯度以及链式法则的知识,以帮助读者快速掌握深度学习中的微积分知识。
2.2.1 导数
假设存在一个连续的光滑函数 ,能够将实数 映射为另一个实数 。根据函数 连续性 的定义,当输入 发生微小变化时,函数的输出 也只会发生微小的变化。也就是说,当 增大了一个很小的因子 ,会导致 也发生很小的变化 ,这个过程可以表示为:
此外,由于函数是光滑的,因此在某个点 附近,如果 足够小,则可以将 近似为斜率为 的线性函数。
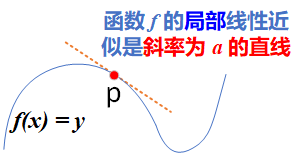
图2.2.2 函数f在p点的导数
此时,输出的变化 可以表示为 ,即:
显然,只有当 足够接近 时,这个线性近似才有意义。我们将切线 的斜率 称为函数 在 点的 导数(derivative)。当 为负值时, 在 点附近的微小变化将导致函数 减小;类似地,当 为正值时, 在 点附近的微小变化将导致函数 增大。函数增大或减小的快慢由导数 的绝对值的大小决定。
以上是有关导数的直观理解,下面我们用更准确的方式对导数进行定义。对于一个定义在实数域上的实值函数 ,其输入和输出都是标量。如果 在点 的某个邻域 内,其极限都存在,且该极限被定义为:
那么,则称函数 在点 处是 可导(derivable) 或 可微(differentiable) 的。函数 称为 在点 处的导数。导数在几何空间的意义就是 图2.2.2 所描述的函数曲线在曲线上某一点的切线的斜率。通常情况下,切线在某一点的斜率都是一个固定的标量值。所以,公式2.2.6 所描述的导数 可以解释为函数 在点 处的瞬时(instantaneous)变化率。注意,所谓瞬时变化率是基于 中的微小变化 而言,且 。
如果 在一个开区间内的每个值都是可微的,我们就称函数 在此区间内是可微的。对于每个可微函数 (可微 的意思是“可以被求导”。例如光滑的连续函数),都存在一个导函数 ,将 映射为曲线 在该点的局部线性近似(切线)的斜率。
下面,让我们来熟悉一下导数的几个等价符号。给定 ,其中 和 分别是函数 的自变量和因变量,存在以下等价关系:
在以上等式中,符号 和 是微分运算符,表示 微分 操作。理论上,对于每一个函数,我们都可以通过 公式2.2.6 所定义规则求取函数的导数。表2.2.1 中列出了一些常用的初等函数的导数。
表2.2.1 常用初等函数及其导数
函数 |
原函数 |
导数 |
|---|---|---|
| 常数 | ||
| 幂函数 | ||
| 指数函数 | ||
| 指数函数(底为 e) | ||
| 对数函数 | ||
| 对数函数(底为 e) | ||
| 正弦函数 | ||
| 余弦函数 | ||
| 正切函数 |
在实际应用中,绝大多数函数都不是简单的初等函数,而是由各种初等函数组成的复合函数。对于复合函数的求导,可以使用如下常用法则。假设函数 和 都是可微的,C是一个常数,则:
-
常数乘法法则:
-
加法法则:
-
乘法法则:
-
除法法则:
在熟记了初等函数的导数,并熟练运用复合函数的求导规则后,我们就可以求解任意复杂函数的导数了。
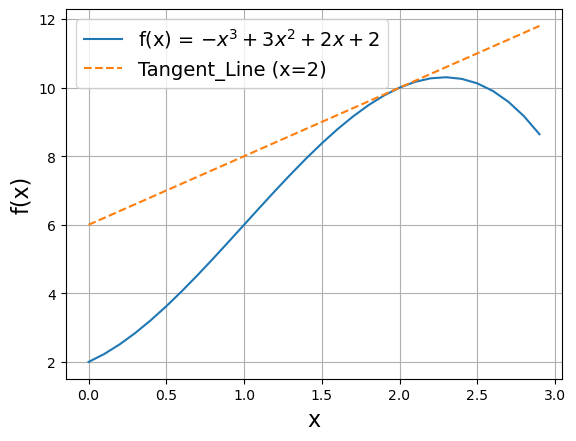
为了更好地理解导数的概念,让我们一起使用代码来研究并验证函数 的求导问题。令 ,且让 逐渐接近0,按照 公式2.2.6 计算可得 。
# codes02029_A_example_of_derivative # 1. 定义待优化函数 def f(x): return -x ** 3 + 3 * x ** 2 + 2 * x + 2 # 2. 定义求导定义函数 def df(f, x, dx): return (f(x+dx) - f(x)) / dx # 3. 计算优化函数的极限(导数) x0 = 2 dx = 0.1 for i in range(6): print("dx={:.5f}, d(fx)={:.5f}".format(dx, df(f, x0, dx))) dx *= 0.1
dx=0.10000, d(fx)=1.69000 dx=0.01000, d(fx)=1.96990 dx=0.00100, d(fx)=1.99700 dx=0.00010, d(fx)=1.99970 dx=0.00001, d(fx)=1.99997 dx=0.00000, d(fx)=2.00000
在 程序清单2.2.2 中,我们首先构造待优化函数 以及求导函数 。接下来,我们使用循环结构计算待优化函数 的极限。从输出结果可以看到,函数 在点 处的导数趋近于2,这个结果与使用 公式2.2.6 所获得的解析解相同。当 时,此导数也是曲线 的切线 的斜率,切点为(2, 10)。下面,我们使用matplotlib库对这个解释进行可视化。
# codes02030_DerivativeVisualization import numpy as np import matplotlib.pyplot as plt x = np.arange(0, 3, 0.1) plt.plot(x, f(x), x, 2*x+6, '--') plt.legend(['f(x)', 'df(x=2)']) plt.ylabel('f(x)', fontsize=16) plt.xlabel('x', fontsize=16) plt.grid()
2.2.2 偏导数
到目前为止,我们只讨论了仅包含一个参数的微分。在深度学习中,函数通常依赖于许多变量的共同作用。因此,我们还需要将微分的概念推广到 多元函数(multivariate function) 的概念中。
对于一个包含 个元素的多元函数 ,我们可以只针对它的第 个自变量求导。在求导过程中,将其他自变量视为常数,此时就可以得到 关于第 个参数 的 偏导数(partial derivative):
为了计算 ,我们可以简单地将除 以外的其他参数 看作常数,并计算 关于 的导数。对于一个 元函数 ,它可以包含 个偏导数,分别记为:。与导数类似,偏导数也有多种表示方式,以下表示是等价的:
2.2.3 梯度
梯度(gradient) 是张量运算的导数,它是一元函数的导数概念向多元函数的导数的推广。一般来说,多元函数都以张量作为输入的函数,我们可以通过连结这个多元函数对所有参数的偏导数来获得多元函数的梯度。具体而言,设函数 的输入是一个 维向量 ,并且输出还是一个标量。此时,函数 关于输入向量 的梯度是一个长度为 的偏导数向量:
其中, 在没有歧义时,可简化为 。在进行多元函数的微分计算时,若输入 是一个 维度向量,则以下规则常被使用:
- 对于所有矩阵 ,都有
- 对于所有矩阵 ,都有
- 对于所有方阵 ,都有
- 对于任意矩阵 ,也存在
梯度在深度学习的优化算法中具有重要作用。假设存在一个输入向量 和一个目标 ,并且存在一个权重矩阵 能够唯一地将输入映射成输出 。此时,我们可以设置一个损失函数loss(),来计算模型的预测值 与目标真实值 之间的距离,这个距离通常也称为损失值,它代表的是预测值和真实值的相似程度,表示为:
我们最终的目标就是通过不断地优化权重矩阵 ,使得损失值尽量趋近于0。换句话说,模型的训练就是在最小化损失函数的输出,并获取一组关于模型的最优参数 ,即:
假设输入 和目标输出 保持不变,那么我们可以将 映射到损失值的过程看作是一个优化函数 ,表示为:
不难看出,优化函数 的目标就是 公式2.2.16 所描述损失值最小时的权重参数 。
我们不妨假设 的当前值为 ,此时,函数 在 点的导数 是一个形状与 相同的张量。该导数的每个元素 都表示改变 时,损失值变化的大小和方向。
在 2.2.1 小节中,我们介绍过单变量函数 的导数可以看作是曲线函数 的斜率。类似地, 也可以看作是曲平面函数 在 附近的 曲率(curvature) 的张量。换句话说,如果我们将 看作是单变量函数在 点的导数;那么, 就是多元函数在 附近梯度。
与函数 的导数类似,关于张量 的函数 ,也可以通过将 向梯度的反方向移动来减小 ,例如:。其中,步长 是一个很小的比例因子,与单变量函数 中的 类似,表示对梯度执行的微小变化,该变化不能距离 太远。也就是说,如果瞬时状态 沿着梯度的反方向移动,直观上看,它在曲线上的位置将会变得更低。这个过程使得loss_value变得更小,这意味着函数向着我们最终的优化目标又迈进了一步。
2.2.4 链式法则
在前面的算法中,我们假设函数都是可微的,因此理论上可以使用解析法来明确地计算导数。然而,在实践中,由于神经网络等深度学习算法通常都是由许多连接在一起的张量运算构成的多元 复合函数(composite function),因此,上面的方法是很难找到梯度的。幸运的是,微积分中的链式法则可以用来微分复合函数。
设 是实数, 都是从实数映射到实数的函数,并且函数 都是可微的,根据链式法则:
或表示为:
进一步,我们可以将这种标量的情况扩展为更一般的场景,即函数包含任意数量变量的情况。假设 ,且 是从 到 的映射。如果 ,那么:
在深度学习中,应用于神经网络梯度值计算的链式法则算法称为 反向传播算法(back-propagation) 或 反式微分(reverse-mode differentiation)。反向传播算法从最终的损失值开始,从最顶层反向作用到最底层,利用链式法则计算每个参数对损失值的贡献大小,并根据这个贡献值来进行梯度的更新。在所有参数的共同作用下,损失值不断减小,模型得以优化。这个过程就是基于梯度下降的模型训练,我们将在后续章节进行详细介绍。
2.4.7 自动微分
正如前面所介绍,求导几乎是所有深度学习优化算法的关键步骤。虽然针对单个神经元的求导很简单,只需要一些基本的微积分知识,但对于由数以亿计的神经元所构建的复杂模型来说,手工进行梯度更新是一件非常痛苦且不现实的事情。
事实上,深度学习界在某种程度上已经与更广泛的计算机科学界隔离开来,并在很大程度上发展了一系列自己关于如何进行微分的文化态度(Goodfellow, 2016)。一般来说,大多数深度学习框架都实现了自动计算导数的 自动微分(automatic differentiation) 机制来加速导数的求解。我们前面所提到的反向传播算法就是自动微分的一种方法,它是一种称为 反向模式累加(reverse mode accumulation) 的更广泛类型技术的特殊情况。其他方法以不同的顺序来计算链式法则。但是,确定一种使得计算开销最小的计算顺序是非常困难的,找到计算梯度的最优操作序列是NP完全问题 (Naumann, 2008)。
在实际应用中,这些深度学习库都会构建一个 计算图(computational graph) 来跟踪哪些数据是通过哪些操作组合起来并产生输出的。这意味着,反向传播算法会去跟踪整个计算图来填充关于每个参数的偏导数。它首先将梯度附加到想要对其计算偏导数的参数上,然后记录目标值的计算结果,再执行它的反向传播函数,并访问得到的梯度。
不管怎么说,自动微分为我们实现深度学习模型的梯度更新提供了一种强有力的方法,它是深度学习模型能够良好运行的基础。但这些知识超出了本书的内容,有兴趣的读者可以查阅相关文献 (Zhang, 2021;Goodfellow, 2016)
2.4.7 小结
微分和积分是微积分的两个不同分支,它们是深度学习中最重要的两个基本概念,被用来描述模型参数的变化。前者描述了模型参数的变化情况,并被应用于解决模型的优化问题;而后者体现的是这些参数的总体变化情况,反映了预测值向真实值逼近的过程。在微积分中,导数可以被解释为函数相对于参数的瞬时变化率。梯度是一元函数导数向多元函数的推广,它是张量运算的导数,也是多变量函数相对于其所有变量的偏导数。链式法则被用来解决多层复合函数的微分问题。
在深度学习中,模型的训练是一个不断优化参数的过程。对于损失函数 来说,我们的目标是将 最小化。此时,只需要知道损失函数的导数 ,就可以解决损失函数 最小化的问题。因为导数完全描述了改变 后,函数 会如何变化。因此,如果希望减小 的值,只需要将 沿着导数的反方向移动一小步就可以了。在实际应用中,如果我们将变量 扩展为高维空间的张量 ,并且将函数 定义为损失函数 。以上最小化函数 的过程,就是变成了基于梯度下降算法的模型优化的过程。
2.4.8 练习
- 绘制函数 和其在 处的切线图像。
- 求函数 的梯度。
- 设 可微,且 ,求 。