2.1 神经网络的基础：线性代数

🏷sec0201_Mathematics_LinearAlgebra

线性代数是数学的重要分支学科，它不仅仅是很多其他数学知识的基础，也为人们提供了可以应用于不同专业领域的通用分析和解决问题方法，特别是在科学与工程领域中被广泛应用。在现代数学分析中，最核心的要素是方程与函数，其中最简单的是一次方程和一次函数。线性代数中的“线性”代表的是“一次”，“代数”则代表了最基本的“加减乘除”。顾名思义，线性代数的主要任务就是求解和处理一次方程和一次函数。所以，线性代数也被认为是最简单的数学。在大多数计算机领域中，数据处理主要面向离散数据，而线性代数擅长于处理连续数据，因此很多计算机科学家都很少接触线性代数。然而，对于机器学习的相关算法来说，大量的函数逼近、最优化求解等运算都可以利用连续函数的思想来处理。因此，在介绍人工智能的相关算法之前，我们还是需要集中讨论一些必备的线性代数知识。

线性代数研究的主要内容包括线性方程组、矩阵、向量空间、行列式和方阵的特征值与特征向量等。这些看起来繁琐的运算都可以归结为两种最简单的运算：矩阵初等变换和矩阵乘法。理论上来说，复杂的运算都可以理解为简单运算的反复应用，而最困难的重复运算，理论上又都可以交给计算机去完成，这为我们使用线性代数去解决问题提供了便利。因此，人的任务不再象过去一样聚焦于如何获得表达式的计算结果，而是转变成如何将纷繁复杂的世界中千差万别的复杂问题转换成最简单的运算组合。借助于计算机强大的并行处理能力，这些简单但繁琐的运算将被高效地计算，并最终经过具象化后还原到现实世界中。例如，现在最流行的卷积神经网络的每个神经元只负责一个最简单的线性运算，数以亿计的神经元组合在一起就可以完成各种复杂的任务。

本小节所涉及的内容主要是机器学习所需要应用的数学基础知识，如果你已经很熟悉线性代数，那么你可以轻松地跳过本节。如果你已经了解这些概念，但是需要回顾一些重要公式，那么也可以使用本书来进行索引学习。如果你没有接触过线性代数，那么本节可以为你储备这些基础知识提供帮助。本节略去了很多重要但对于理解机器学习和深度学习非必需的知识，不过我们仍然强烈建议你参考其他专门讲解线性代数的文献，例如：（Strang, 2003；Shilov, 1977），或者有关矩阵论的文献 《The Matrix Cookbook》（Petersen, 2006）。

2.1.1 数据表示

线性代数为线性方程提供了一种简洁的表示和操作方法，在各种机器学习算法中被广泛应用。首先，让我们来看一个简单的例子，考虑如下的一个方程式：

$$\begin{equation} \tag{2.1} \begin{cases} &4x_1-5x_2 & = & -13 \\ -&2x_1+3x_2 & = & 9 \nonumber \end{cases} \end{equation}$$

这是一个包含两个未知变量和两个等式的方程组。对于这样简单的方程组，我们可以很容易地获得未知变量$x_1$和$x_2$的解，并且知道这组解是唯一解。在矩阵的表示法中，可以将该方程组简化为如下表达：

$$\begin{equation} \tag{2.2} \begin{aligned} & Ax = b \\ & A = \begin{bmatrix} 4 & -5 \\ -2 & 3 \end{bmatrix}, b = \begin{bmatrix} 13 \\ -9 \end{bmatrix} \\ \end{aligned} \end{equation}$$

正如我们所见，这种简洁的表示方法有很多的优点，包括方便计算，容易理解，以及节省书写空间等。在后续的学习中，我们会体会到更多这种简洁表示法所带来的优势。

在以机器学习为目标的线性代数体系中，我们首先需要了解的是如何进行数据表示，一种好的数据描述方法对于学习和使用机器学习算法是极具促进作用的。正如Google著名的深度学习框架 TensorFlow 的名字，几乎所有的机器学习和深度学习算法都可以看作是数据 张量（tensor） 在各个模块间以 流动（flow） 的方式进行信息传递。因此，张量也被作为本书主要介绍的数据表示方法。张量可以被理解为一种数字数据的容器，它所包含的数据几乎都是数值数据。我们所熟知的标量、向量和矩阵等数学概念，也都可以使用张量来进行描述。例如，上面我们用来描述方程的矩阵也被称为二阶张量。

为了便于理解，下面我们先从代数的角度来简要介绍标量、向量和矩阵的概念。之后，我们再在高维空间中将这些物理量统一到张量的概念体系中。

2.1.1.1 标量

在日常生活中，我们接触最多的是标量，例如某商品的价格是人民币$2.3$元，今天的气温$21℃$。严格地说，标量(scalar) 是一个只具有数值大小，而没有方向的独立的量。标量可以有正负之分，因此它也被称为“无向量”。它是一个在坐标变化下始终保持不变的量。如果我们需要计算身体质量指数中的理想体重，则可以用表达式 “理想体重 $=h-105$” 来表示。其中，数值105就是标量值，而符号 $h$ 称为变量（variable），它是一个表示身高的未知的标量值。

习惯上，我们使用 斜体的小写英文字母 来表示标量变量，例如：$m$, $n$, $i$ 等。在进行标量的定义时，明确说明标量的数据类型通常是有必要的。例如，在对实数标量进行定义时，我们会“令 $k \in \mathbb{R}$ 表示一条直线的斜率”；在定义自然数标量时，我们会“令 $n \in \mathbb{N}$ 表示元素的数量”。在上面的表示中，$\mathbb{R}$ 表示所有连续的实数空间, $\mathbb{N}$ 表示自然数空间。符号 $\in$ 称为“属于”，它表示“是集合中的成员”，例如 $x,y \in \{0,1\}$ 可以用来表示 $x$, $y$ 的取值是0或1中的一个数字。在线性代数中，我们研究的对象通常都不是标量，而是由多个数组成的数组，但是标量经常以这些对象中的最小元素形式存在，正如前面例子中的数字0和1。

在Python中，我们通常将包括标量在内的所有张量数据都存储在一个多维 Numpy 数组中。在 Numpy 中，数据类型为float32以及float64的数字所代表的数据都是标量数据，你可以使用函数 np.array() 来对它进行定义。如果使用 Paddle 工具包，则可以直接用 paddle.to_tensor() 函数以张量的形式对它们进行定义。下面的代码将分别使用 Numpy 数组和 Paddle数据类型来实例化两个标量，并执行一些熟悉的算术运算，包括加法、减法、乘法、除法和指数。

# codes02001_scalar_numpy
import numpy as np

x = np.array(12.0)
y = np.array(-1.5)
print(x + y, x - y, x * y, x / y, x**y)

(10.5, 13.5, -18.0, -8.0, 0.024056261216234408)

# codes02002_scalar_paddle
import paddle

x = paddle.to_tensor([12.0])
y = paddle.to_tensor([-1.5])
print(x + y, x - y, x * y, x / y, x**y)

(Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [10.50000000]),
 Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [13.50000000]),
 Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [-18.]),
 Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [-8.]),
 Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [0.02405626]))

2.1.1.2 向量

向量（vector），又称为“欧几里得向量、一维数组、矢量、几何向量”，它是一种具有大小和方向的量，可以在坐标系中形象化地表示为带箭头的线段。箭头所指的方向代表了向量的方向，线段的长度代表了向量的大小。在代数系统中，向量是一个数列，数列中的数称为元素（element）或分量（component），它们可以是标量，也可以是向量或矩阵。数列中的元素都是有序的，通过次序中的索引，我们可以确定每个单独的元素。当使用向量表示数据集中的样本时，它们的值就具有一定的现实意义。例如，我们正在训练一个用来预测某地区房价的模型，可能就会将每幢房子与一个向量相关联，其分量与建筑年代、建筑风格、朝向、周边环境、物业、配套设施等因素相对应。如果我们正在研究结核病传染病与个体的关联性时，可能会用一个向量来表示每个个体的基本信息，其分量为性别、年龄、职业、既往TB病史、耐药性、病原学检测结果等。

在数学表示法中，向量通常记作 粗斜体的小写英文字母，例如：$\boldsymbol{a}$, $\boldsymbol{x}$ 等。向量中的元素可以使用 带下标的斜体的小写英文字母 来表示，例如：向量 $\boldsymbol{a}$ 的第1个元素和第 $i$ 个元素分别记作 $a_1$, $a_i$。与标量相似，在定义向量的时候，我们通常也需要显式地说明向量中的元素是什么数据类型。如果每个元素都属于实数，且该向量包含 $n$ 个元素，那么该向量就是属于实数集的 $n$ 次笛卡尔乘积构成的集合，记作 $\mathbb{R}^n$。至此，我们可以用 $\boldsymbol{x} \in \mathbb{R}^n$ 来表示一个包含 $n$ 个元素的向量。一般来说，向量可以具有任意长度，这取决于机器的内存限制。与标量类似，我们同样可以使用Numpy数组或者Paddle类来定义向量。

# codes02003_vector_numpy
import numpy as np

x = np.array([1, 3, 5, 7, 9]) # 定义向量
print(x)                      # 输出向量
print(x[3])                   # 输出向量的第3个元素

[1 3 5 7 9]
7

# codes02004_vector_paddle
import paddle

y = paddle.arange(6)         # 定义向量
print(y)                     # 输出向量
print(y[3])                  # 输出向量的第3个元素

Tensor(shape=[6], dtype=int64, place=Place(gpu:0), stop_gradient=True, [0, 1, 2, 3, 4, 5])
Tensor(shape=[1], dtype=int64, place=Place(gpu:0), stop_gradient=True, [3])

不难看出，在上面代码中，向量 $\boldsymbol{x}$ 包含5个元素，我们通常称其为5D向量（五维向量）。注意不要将五维向量和五维张量弄混，它们两者的维度的概念是不相同的！由于向量只存在一个方向，因此即使是五维向量它也只具有一个方向（轴）。五维向量的5D表示该向量沿着这个唯一轴的方向存在5个分量，习惯上我们将向量的分量用维度来表述。理论上来说，向量在一个方向上是可以包含任意多个维度的，也即它可以包含任意多的元素，只要计算机的内存足够大。而五维张量则表示它有5个轴，沿着每个轴的方向也都可以由任意多个维度构成。因此，维度（demensionality） 既可以表示沿着某个轴方向上的元素个数（例如5D向量），也可以表示张量中轴的个数（例如5D张量）。在这里，维度的表述难免会令人感到混乱，所以我们建议在技术上使用更准确一些的说法，即使用阶数来表示张量的维度。换句话说，对于一个5D张量，更准确的说法是 5阶张量，张量的阶数就是轴的个数。在第 2.1.1.4 小节中，我们会详细讨论这个问题。

通常，一个向量 $\boldsymbol{x}$ 都默认表示为一个列向量（换句话说，它相当于一个包含 $n$ 行和1列的矩阵），本书也遵循这种规范。在代数系统中，列向量可以用一个方括号包围的纵列元素集合表示：

$$\begin{equation} \tag{2.3} \boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}. \end{equation}$$

如果我们需要显示地表达一个行向量（即一个包含1行和 $n$ 列的矩阵），我们可以用符号 $\boldsymbol{x}^T$ 来表示，其中 $\boldsymbol{x}^T$ 表示 $\boldsymbol{x}$ 经过转置运算后的结果。

$$\boldsymbol{x}^T = [x_1, x_2, \cdots, x_n] \tag{2.4}$$

对于向量 $\boldsymbol{x} \in \mathbb{R}^n$ 来说，序列 $x_1, x_2,..., x_n$ 表示该向量的元素，其中第 $i$ 个元素可以用符号 $x_i$ 来表示。在Python代码中，我们可以通过索引来访问张量中任意一个元素。

print(x[3])

7.0

print(y[3])

Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [3.])

2.1.1.3 矩阵

矩阵（matrix），是一个按照长方阵型排列的实数集合，其概念最早来源于由方程组的系数及常数所构成的方阵（注意矩阵也可以表示复数的集合，但在机器学习中几乎用不到）。矩阵的概念是由19世纪英国数学家阿瑟·凯莱（Arthur Cayley）首先提出，它是高等代数学中最常见的工具，也常被用于统计分析等应用数学中。我们通常所说的矩阵都是特指二维数组，二维数组中的每个元素都由两个索引唯一确定（在实际应用中，也经常使用三维矩阵等更高维度的矩阵）。通常我们使用 粗斜体的大写英文字母 来书写矩阵，例如 $\boldsymbol{A}, \boldsymbol{B}$ 等。如果一个所有元素都是实数的矩阵包含 $m$ 行 $n$ 列，那么我们可以用符号 $\boldsymbol{A} \in \mathbb{R}^{m×n}$ 来定义和表示这个矩阵。对于矩阵 $\boldsymbol{A}$ 中的每一个元素，可以使用 不加粗的斜体英文字母 来表示，如 公式2.5 那样，我们可以简单地使用 $a_{ij}$（或 $A_{ij}$）来表示矩阵 $\boldsymbol{A}$ 第 $i$ 行、第 $j$ 列的元素。为了表示起来简单，只有在必要的时候才会使用逗号插入到单独的索引中，例如：$a_{3,2i}, a_{2i+1, 3j-1}$。当需要明确表示矩阵中的每一个元素时，我们可以将矩阵的元素列在方括号括起来的方阵中：

$$\begin{equation} \tag{2.5} \boldsymbol{A} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix}. \end{equation}$$

对于任意 $\boldsymbol{A} \in \mathbb{R}^{m×n}$，$\boldsymbol{A}$ 的形状是（m, n）或 $m×n$。当矩阵的行数和列数相同时，该矩阵的形状将变为正方形，此时，它被称为方阵（square matrix）。

在调用函数来实例化矩阵时，我们可以通过指定矩阵的两个维度分量 $m$ 和 $n$ 来创建一个形状为 $m×n$ 的矩阵。矩阵第一个轴上的元素称为 行（row），第二个轴上的元素称为列（column）。例如，在下面代码中的矩阵 $\boldsymbol{A}$ 中，第一行的元素包括 [0, 1, 2, 3, 4]，第一列的元素包括 [0, 5, 10, 15]。。

# codes02005_matrix_numpy
import numpy as np

A = np.arange(20).reshape(4, 5)
print(A)

[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]
 [15 16 17 18 19]]

# codes02006_matrix_paddle
import paddle

B = paddle.reshape(paddle.arange(20), (4, 5))
print(B)

Tensor(shape=[4, 5], dtype=int64, place=Place(cpu), stop_gradient=True,
       [[0 , 1 , 2 , 3 , 4 ],
        [5 , 6 , 7 , 8 , 9 ],
        [10, 11, 12, 13, 14],
        [15, 16, 17, 18, 19]])

为了简化表示方法，有时候我们可以使用符号“:”来代表一整行或一整列中的所有元素。例如，使用符号 $\boldsymbol{A}_{:,j}$（或使用单下标形式 $\boldsymbol{A}_{j}, \boldsymbol{a}_{j}$）表示矩阵 $\boldsymbol{A}$ 第 $j$ 列（column）的所有元素：

$$\begin{equation} \tag{2.6} \boldsymbol{A} = \begin{bmatrix} \mid & \mid & \mid & \mid \\ \boldsymbol{a}_1 & \boldsymbol{a}_2 & \cdots & \boldsymbol{a}_n \\ \mid & \mid & \mid & \mid \end{bmatrix}. \end{equation}$$

相似地，也可以用 $\boldsymbol{A}_{i,:}$ 或 $\boldsymbol{a}^T_i$ 表示第 $i$ 行（row）的所有元素：

$$\begin{equation} \tag{2.7} y = \boldsymbol{A}x = \begin{bmatrix} — & \boldsymbol{a}_1^T & — \\ — & \boldsymbol{a}_2^T & — \\ — & \vdots & — \\ — & \boldsymbol{a}_m^T & — \\ \end{bmatrix} x= \begin{bmatrix} \boldsymbol{a}_1^T x \\ \boldsymbol{a}_2^T x \\ \vdots \\ \boldsymbol{a}_m^T x \\ \end{bmatrix}. \end{equation}$$

在上面表示第 $i$ 行元素的时候，我们使用了上标符号 $^T$，这种表示方法与前一小节中行向量的表示方法 $\boldsymbol{x}^T$ 是一致的，即 转置（transposition） 运算。简单地说，转置实现了矩阵中行和列的交换。正如通过交换向量的行和列来实现 列向量 向 行向量 的变换。对于 公式2.5 所描述的矩阵 $\boldsymbol{A}$，我们可以使用 $\boldsymbol{B} = \boldsymbol{A}^T$ 来表示其转置矩阵。对于任意 $i$ 和 $j$，都有 $b_{ij} = a_{ji}$。因此，矩阵 $\boldsymbol{A}$ 的转置是一个形状为 $n×m$ 的矩阵：

$$\begin{equation} \tag{2.8} \boldsymbol{A}^T = \begin{bmatrix} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \\ \end{bmatrix}. \end{equation}$$

下面的代码，实现了矩阵 $\boldsymbol{A}$ 的转置矩阵 $\boldsymbol{B}$ 的访问。

np.transpose(A)

array([[ 0,  5, 10, 15],
       [ 1,  6, 11, 16],
       [ 2,  7, 12, 17],
       [ 3,  8, 13, 18],
       [ 4,  9, 14, 19]])

paddle.transpose(A, perm=[1, 0])

Tensor(shape=[5, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
       [[0 , 5 , 10, 15],
        [1 , 6 , 11, 16],
        [2 , 7 , 12, 17],
        [3 , 8 , 13, 18],
        [4 , 9 , 14, 19]])

无论是在机器学习还是在数据分析中，矩阵都是最有用的数据类型之一，它允许我们组织具有不同模式的数据。例如，我们所以定义的矩阵的行可能对于不同的行人，而列可能对应于行人不同的属性。这种机制与常用的电子表格很相似，应该不难理解。尽管向量的默认方向是列向量，但以表格形式存储的数据集矩阵，将每个样本作为行向量进行存储更为常见。这种约定将支持常见的深度学习实践，例如我们可以沿着张量的最外层的轴来访问和遍历小批量的数据样本。

2.1.1.4 张量

1. 张量的基本概念

在人工智能的各种算法中，我们经常会讨论坐标轴超过两维的数组，即数组中的每个元素都分布在超过两个维度的规则网格中。我们称这样的数组为 张量(tensor)。张量是一个定义在一些向量空间和一些对偶空间的笛卡尔积上的多重线性映射。张量的坐标是 $n$ 维空间内有 $n$ 个分量的一种量，其中每个分量都是坐标的函数。在进行坐标变换时，这些分量也依照某些规则做线性变换。为了更好地解释什么是张量，我们先来厘清两个重要的概念：基向量（Basis Vectors） 和 分量（Components）。首先，让我们引入一个最常见的三维空间中的笛卡尔坐标系（Cartesian coordinate system）。在三维笛卡尔坐标系中，$x$, $y$, $z$ 轴方向上分别都存在一个基向量，并且它们的长度都是“1”，且方向与坐标轴一致。

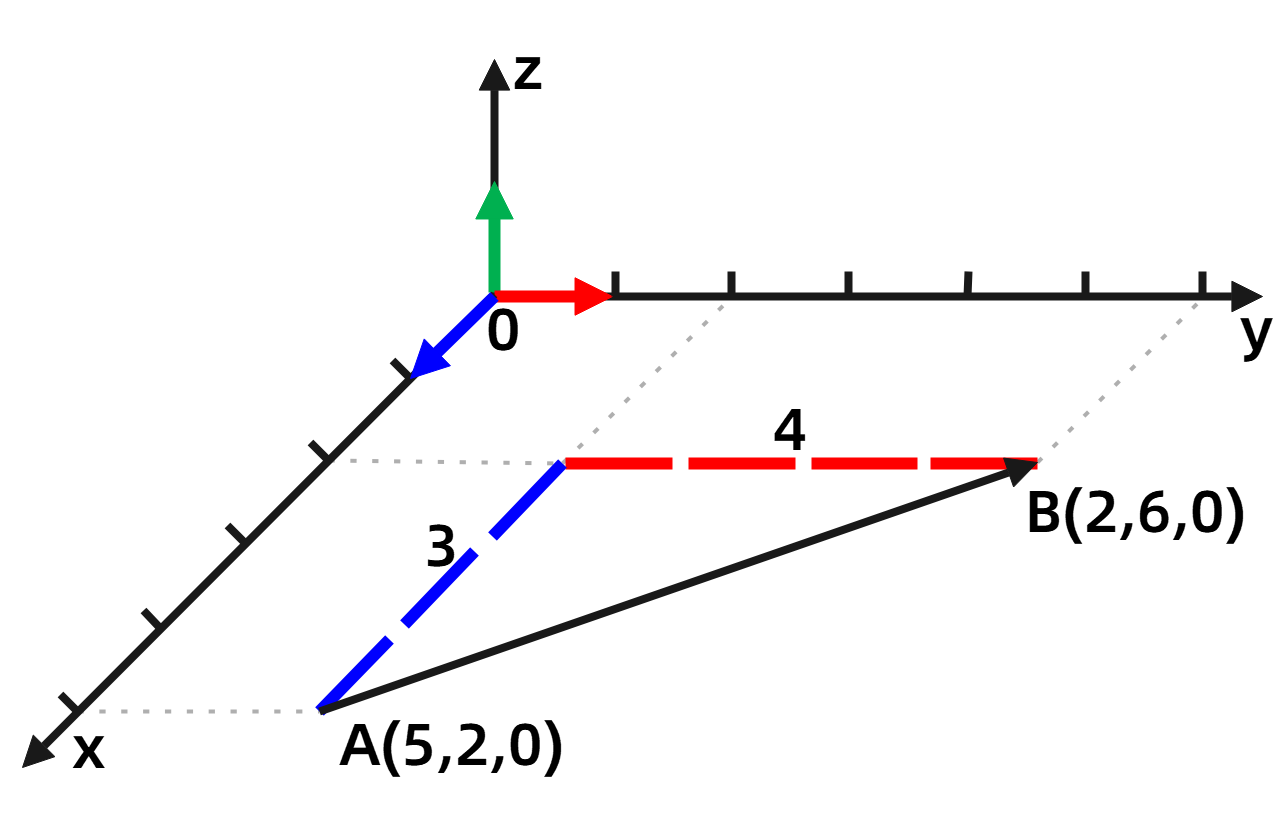
图2-1 笛卡尔坐标系中的向量。蓝、红、绿三个带箭头的短线分别代表x,y,z方向上的基向量，其长度均为1。向量AB位于xy平面中，因此其z坐标为0。

如 图2-1 所示，向量 $\boldsymbol{V}$ 的两个端点分别是 A（5, 2, 0）、B（2, 6, 0），它由3个 $x$ 基向量，4个 $y$ 基向量和0个 $z$ 基向量构成。所以，我们也可以用4个 $x$，3个 $y$ 和0个 $z$ 来表示向量 $\boldsymbol{V}$ 。当 $x$, $y$, $z$ 使用相同的一套基向量（L=1）时，我们只需要用（4, 3, 0）这三个数字就可以表示向量 $\boldsymbol{V}$ 了，而这三个数字就称为向量 $\boldsymbol{V}$ 的分量。注意，此时每个分量都只有一个下标，因为每个分量都只由一个基向量构成，所以我们称向量为一阶张量。

与矩阵的表示方式类似，我们也使用 粗斜体的大写英文字母 来表示张量。例如，当使用 $\boldsymbol{A}$ 表示三维空间中的三阶张量时，$\boldsymbol{A}$ 将具有 $3^3$ 个分量；如果三阶张量存在于 $n$ 维空间，那么张量 $\boldsymbol{A}$ 将具有 $n^3$ 个分量。对于坐标为 $(i, j, k)$ 的元素可以被记为 $\boldsymbol{A}_{i,j,k}$。对于 $n$ 维空间的 $m$ 阶张量 $\boldsymbol{A}$ ，将具有个 $n^m$ 分量，其中 $r=m$ 称为张量 $\boldsymbol{A}$ 的秩或阶数。值得注意的是，张量的分量并非只能是标量，也可以是一个张量。

在构建高阶张量时，可以使用组合多个低阶张量的方法来实现。例如使用多个2D矩阵的组合来构建一个3D张量，下面给出构建一个3D张量的代码示例。

# codes02007_tensor_numpy
import numpy as np

TensorA = np.arange(24).reshape(3, 2, 4)               # 构建张量
print('张量TensorA的维度为：{}'.format(TensorA.ndim))   # 输出张量的维度
print(TensorA)                                         # 输出张量

张量TensorA的维度为：3
[[[ 0  1  2  3]
  [ 4  5  6  7]]
 [[ 8  9 10 11]
  [12 13 14 15]]
 [[16 17 18 19]
  [20 21 22 23]]]

# codes02008_tensor_paddle
import paddle

TensorB = paddle.reshape(paddle.arange(24), (3, 2, 4))  # 构建张量
print('张量TensorB的维度为：{}'.format(TensorB.ndim))    # 输出张量的维度
print(TensorB)                                          # 输出张量

张量TensorB的维度为：3
Tensor(shape=[3, 2, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
       [[[0 , 1 , 2 , 3 ],
         [4 , 5 , 6 , 7 ]],
        [[8 , 9 , 10, 11],
         [12, 13, 14, 15]],
        [[16, 17, 18, 19],
         [20, 21, 22, 23]]])

将多个2D矩阵组合成一个3D数组，可以构建一个3D张量；以此类推，将多个3D张量组合成一个数组，也可以构建一个4D张量。在深度学习中，我们一般需要处理的数据都是0D到5D的张量，我们将在 2.1.4 小节中对这些数据进行介绍。

2. 张量的各种表现形式

为了进一步加深对张量的理解，我们再换一个角度来看看向量、矩阵和张量的关系。回顾前面我们对于“量”这个概念的认知。我们可以使用“一个数”来表示标量，用“一个一维数组”来表示向量，然后用“一个二维数组”来表示矩阵。这种表示方法称为代数方法。如果采用几何方法呢？在几何空间中，标量可以被认为是一维坐标系上的一个点，向量则可以被认为是二维、三维或更高维坐标系中的一个空间点或有方向的线段。

现在，我们有了对张量的基本认识，那么我们是否可以将前面所有的物理量都统一在一起呢？答案是可行的。例如，在三维空间中，可以将标量重新理解和定义为零阶张量$（r=0）$。因为标量是没有方向的，所以它也不存在基向量，这相当于标量的每个分量都是由 $0$ 个基向量构成。如前所述，向量在每个维度上都存在一个分量，并且每个分量都只有 $1$ 个下标（即只存在一个基向量），因此向量可以被定义为一阶张量$（r=1）$。相似地，我们可以将矩阵定义为二阶张量$（r=2）$。下面，我们尝试在三维空间和 $n$ 维空间中逐“阶”而上地构建张量的数据结构。

（1）一阶张量（向量）

假定在三维空间中存在一阶张量 $\boldsymbol{A}$，并且该张量有3个分量，则可以将该张量表示为一个有序的三元数组，或一个 $1×3$ 阶的行矩阵：

$$\boldsymbol{A} = [A_1 A_2 A_3] \tag{2.9}$$

如果一阶张量 $\boldsymbol{A}$ 存在于 $n$ 维空间，那么它就应该有 $n$ 个分量。此时，张量 $\boldsymbol{A}$ 可以表示为一个有序的 $n$ 元数组，或一个 $1×n$ 阶的行矩阵：

$$\boldsymbol{A} = [A_1 A_2 ... A_n] \tag{2.10}$$

在几何空间中，张量 $\boldsymbol{A}$ 可以排列成“一条直线”，即向量，如 图 2-2 所示：

图2-2 一阶张量形象化示意图。每个小立方体表示一个基元素，在n维空间中张量A包含n个分量，即n个基元素。基元素可以是一个标量也可以是一个张量。

（2）二阶张量（矩阵）

在三维空间中，一个二阶张量具有9个分量，可以被表示为一个有序的9元数组或一个$3×3$ 阶的矩阵：

$$\begin{equation} \tag{2.11} \boldsymbol{A} = \begin{bmatrix} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \\ \end{bmatrix}. \end{equation}$$

对于 $n$ 维空间，一个二阶张量有 $n^2$ 个分量，可以表示为一个有序的、包含 $n^2$ 个元素的数组，或表示为一个 $n×n$ 阶的矩阵。

由上面的介绍可以看出，一个二阶张量可以用一个矩阵表示，在几何空间中它可以构成“一个张平面”，如 图 2-3 所示：

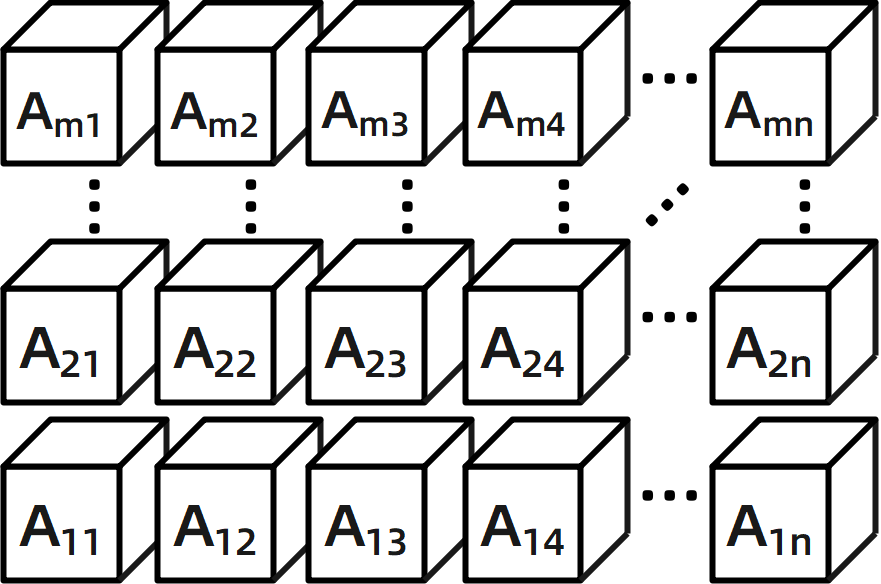
图2-3 二阶张量形象化示意图

（3）三阶张量

按照之前对张量的定义，我们可以知道在三维空间中的一个三阶张量应该具有 $3^3$ 个分量，可以构建出一组包含3个矩阵、每个矩阵包含3个元素的数据体。我们可以将这个数据体设想成一个由“三个平面”搭建而成的“立方体”，如 图 2-4(a) 所示：

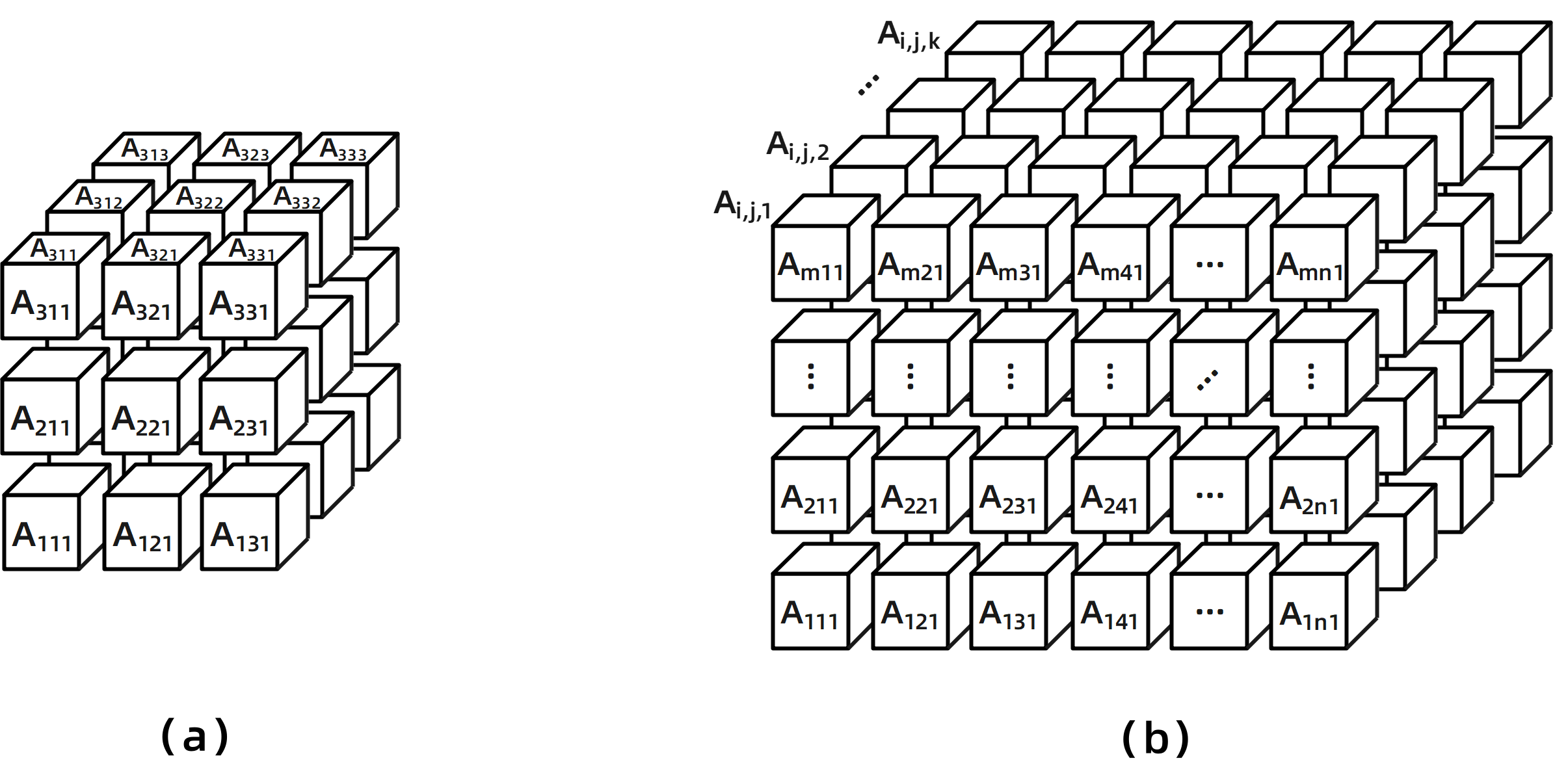
图2-4 三维空间（3×3×3）和 n 维空间（n×n×n）中的三阶张量形象化示意图

相似地，对于 $n$ 维空间来说，一个三阶张量应该具有 $n^3$ 个分量，从而构建出一组具有 $n$ 个矩阵，每个矩阵包含 $n×n$ 个元素的数据体。此时，可以将 $n$ 维空间中的三阶张量设想成一个由“$n$ 个平面”构建而成的“立方体”，如 图 2-4(b) 所示。

（4）四阶张量

对于超过三阶的张量，理解起来稍微有点复杂。在三维空间中，一个四阶张量所具有的分量数量为 $3^4=81$。此时，我们不妨将每 $3^3=27$ 个分量的三阶张量看成是一个独立的“立方体元素”，那么一个四阶的张量就可以被形象化地理解为由3个三阶张量组合（$3×3^3=3^4=81$）在一起的“一组积木”。将这 $3$ 块积木排列成一排，将构建出一个由矩阵构成的“阵列”，如 图 2-5 所示：

图2-5 四阶张量形象化示意图

有了这个类比，在构建 $n$ 维空间中的四阶张量就会变得容易一些。想象一下，不难得出这样的构想，对于 $n$ 维空间中的四阶张量，我们可以将 $n$ 个长宽高都是 $n$ 的立方体积木（即三阶张量）组合在一起构成一组具有 $n$ 个方块的“立方体元素”组合。

（5）高阶张量

对于处于 $n$ 维空间中的五阶张量和六阶张量，我们可以用 图 2-6 所示的立方体来表示。
首先，五阶张量有 $n^5$ 个分量，那么我们可以构建成一个 $n×n$ 的“立方体组合”，即一个 $n$ 行 $n$ 列的结构体，结构体的每个元素都是一个 $n^3$ 的立方体元素。视觉上看，就像“积木块垒起来的一堵墙”。其次，六阶张量有 $n^6$ 个分量，那么，我们可以构建成一个 $n×n×n$ 的“立方体组合”，即一个 $n$ 行 $n$ 列且厚度为 $n$ 的结构体，结构体的每个元素也是一个 $n^3$ 的立方体元素。视觉上看，就像“积木块垒起来的一个方垛”。

图2-6（a）五阶和（b）六阶张量形象化示意图

对于更高阶的张量，例如，$N$ 阶张量，我们可以通过逐层地进行积木的组合，先从一阶张量开始，构建一排一阶张量形成的二阶张量，再构建成方阵形式的三阶张量；然后将三阶张量看成是一个方块元素来构建形如“一排方块”的四阶张量，再到“一堵墙”、“一个方垛”；后再将这个“方垛”看成是一个元素，继续构建“一排方块”，再到“一堵墙”、“一个方垛”，依次类推下去。对于手工计算和思维认识来说，构建高阶张量是一件非常恐怖的事。幸运的是，计算机最擅长的就是处理这类迭代问题，只要不是无限不可解的问题，计算机总是能够获得理想的结果。当然，处理时间还需要看计算机的硬件配置情况，比如今天流行的GPU处理器就特别适合用来做这类重复但是简单的工作。

张量是一种通过基向量和分量组合来表示物理量的方法，由于基向量具有丰富的组合，因此张量也可以用来描绘非常丰富的物理量。比较特别的是，张量所描述的物理量是不随观察者或参考系的变化而变化的。当参考系发生变化时，由于基向量的变化，张量的各个分量也会随之而变化。最终的结果就是基向量和分量的组合始终保持不变，也即张量保持不变。由于张量具有如此强大的表示能力，且具有高度不变性，所以，它能够有效地表示宇宙间的万物。著名数学家Lillian R. Leber将张量称为 “The fact of the universe”。

3. 张量的关键属性

一般来说，张量可以由以下三个关键属性来定义。

• 维度和轴（阶）：向量可以理解为一个由数字组成的一维数组，与所有数组都有长度相同，每个向量也都有长度属性。在代数体系中，如果一个向量 $\boldsymbol{A}$ 由 $n$ 个标量值构成，那么则可以称该向量的维度为 $n$，该向量可以表示为 $\boldsymbol{A} \in \mathbb{R}^n$。简单地说，向量的长度通常称为向量的 维度（dimension）。与向量只有一个方向不同，矩阵可以向两个方向进行延申，每个方向上都可以包含任意多个元素。所以，矩阵就称为2D张量。此处，矩阵的方向数量就称为矩阵的 轴数（axis） 或 阶数（rank）。类似地，三阶张量（3D张量）包含3个轴，四阶张量（4D张量）包含4个轴。我们前面提到，维度这个概念在不同的上下文中往往会有不同的内涵，这常常会使人感到困惑。为避免误解，我们再次明确一下：向量或轴的维度用来表示向量或轴的长度，即向量或轴的元素个数，也即分量大小。张量的维度用来表示张量所具有的轴数，而张量的某个轴的维度则表示该轴的长度（或元素的个数）。在 Numpy 中，可以使用 ndim 属性来获取张量的轴数。

• 形状：张量的 形状（shape） 是对张量各个维度分量大小的描述，一般使用一个整数元素组进行表示，该元素组列出了张量沿每个轴的维度大小（元素个数）。例如，程序清单2-4 中矩阵B的形状为（4，5），程序清单2-6 中3D张量的形状为（3，2，4）。对于只有一个轴的张量（向量），它的形状只包含一个元素，例如（5，）。对于标量数据，由于其轴数为零，因此其形状为空，即（）。注意，在不同的深度学习工作包中，输出的表达方式略有不同。

• 数据类型：张量的数据类型是指张量中所包含的数据元素的类型，常见的数据类型包括整型(int32，int64)和浮点型（float32，float64）等。在极少数情况下，你可能会见过字符型（char）张量。但在深度学习的实践中，几乎不会出现，包括Numpy在内的其他数据处理和深度学习库都不支持字符型张量。

为了具体说明这些关键属性，我们使用一个真实的数据集（MNIST手写数字数据集）来进行观察。

# codes02009_tensor_KeyAttributes_numpy
from sklearn.datasets import fetch_openml

mnist = fetch_openml('mnist_784', version=1, parser='auto', cache=True)
mnist_train = mnist['data']

print('训练数据的轴数为：{}'.format(mnist_train.iloc[0].ndim))

训练数据的轴数为：1

print('训练样本的形状为：{}'.format(mnist_train.iloc[0].shape))

训练样本的形状为：(784,)

print('训练样本的数据类型为：{}'.format(mnist_train.iloc[0].dtype))

训练样本的数据类型为：int64

# codes02010_tensor_KeyAttributes_paddle
import paddle
from paddle.vision import transforms

trans = transforms.ToTensor()
mnist_train = paddle.vision.datasets.MNIST(mode="train", transform=trans)

print('训练数据的轴数为：{}'.format(mnist_train[0][0].ndim))

训练数据的轴数为：3

print('训练样本的形状为：{}'.format(mnist_train[0][0].shape))

训练样本的形状为：[1, 28, 28]

print('训练样本的数据类型为：{}'.format(mnist_train[0][0].dtype))

训练样本的数据类型为：paddle.float32

4. 张量的常用操作

在机器学习的任务中，数据来源通常是多种多样的，所以我们习惯于将待处理的数据都规范为特定维度的张量。例如，在不考虑数据批量化时，彩色图像可以被看成是一个包含 [C, H, W] 三个维度的三阶张量，其中C表示图像包含红、绿、蓝三个颜色通道（或者说三个分量），H和W分别表示图像的高度和宽度。对于视频数据来说，它们可以被看作是一个包含时间帧、每一帧图像的颜色通道、高度和宽度四个维度的四阶张量。

在现实世界中，我们已经习惯了这些数据的常见形态，但在获取这些不同类型数据的原始数据时，可能会存在多种多样的模式。因此，我们一般都需要手动对这些数据进行一定的调整，将它们转换为常用的数据张量形态。常用的张量操作包括 索引（indexing）、切片（slicing）、连接（joining）、换位（mutating） 和 变形（reshaping） 等。

（1）索引

关于张量 索引（indexing） 的方法，我们在前面已经简要介绍过。总结一下，在代数系统中，我们使用从1开始的连续编号来访问张量的元素；而在大多数编程环境中，我们则通过从0开始的连续编号来访问张量的元素。例如，$\boldsymbol{A}_{4,5}$ 和 $\boldsymbol{A}[3,4]$ 分别表示代数系统和Python编程环境中二阶张量 $\boldsymbol{A}$ 的第4行、第5列的元素。

# codes02011_indexing
import numpy as np

# 1. 构建一个4行5列的2D张量
A = np.arange(20).reshape(4, 5)

[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]
 [15 16 17 18 19]]

访问张量 $\boldsymbol{A}$ 的第4行，第5列的元素

# 2. 使用索引访问第4行、第5列的元素
print(A[3,4])

19

（2）切片

在前面的例子中，我们使用变量 mnist_train[0][0] 来获取沿着第一个轴和第二个轴的特定元素。这种使用索引来选择张量特定元素的方法称为 切片（slicing）。如图 2-7 所示，我们给出了两种应用于图片和视频的常见切片方式，一种是按照某一通道轴进行切片，获取该轴的部分通道，其他轴不变（程序清单 2-9）；另一种是对样本的高和宽进行局部切片，获取原始样本的一个局部区域（程序清单 2-10）。

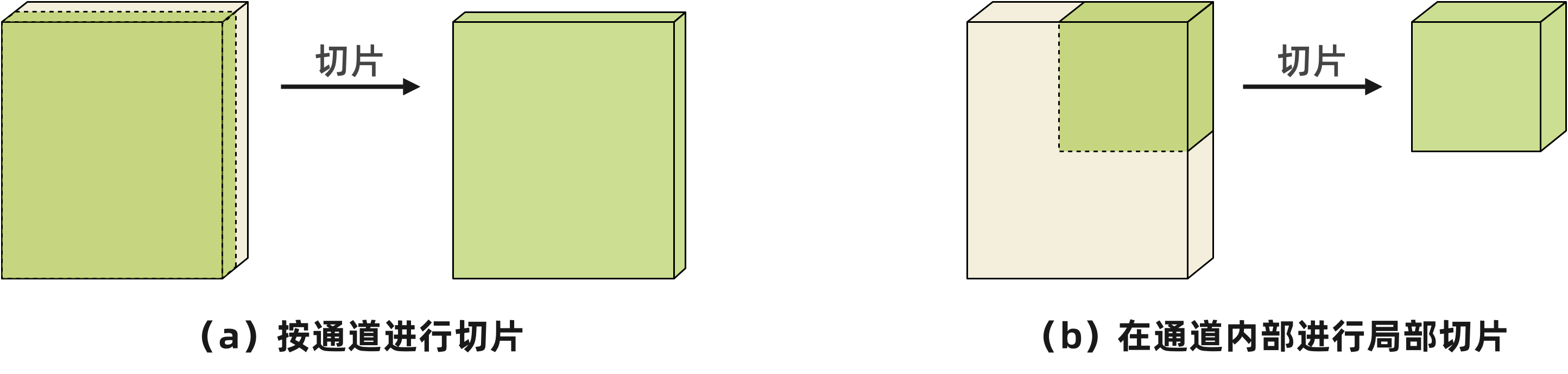
图2-7 张量切片

下面的例子用于提取MNIST数据集中第0~100个数字样本（不包括第100个），并将其保存在一个（100，28，28）的数组中。

# codes02011_tensor_slicing
import numpy as np
# 1. 默认状态导入整个目标张量
my_data = np.zeros([100, 28, 28])    # 初始化一个与目标尺度相同的张量
for i in range(0, 100):
    my_data[i,:, :] = mnist_train[i][0]
print(my_data.shape)

(100, 28, 28)

以上代码使用默认标签进行索引。在不指定轴的维度范围时，程序会默认索引轴的所有维度。下面是两种更为复杂的写法，它们沿着张量每个轴的起始索引和结束索引进行切片。在Python语法中，符号 “:” 等同于选择轴所有的维度。

# 2. 使用“:”方式导入整个张量
my_data1 = np.zeros([100, 28, 28])    # 初始化一个与目标尺度相同的张量
for i in range(0, 100):
    my_data1[i,:, :] = mnist_train[i][0][:,:,:]
print(my_data1.shape)

(100, 28, 28)

# 3. 通过指定起始索引和结束索引来导入整个张量
my_data2 = np.zeros([100, 28, 28])    # 初始化一个与目标尺度相同的张量
for i in range(0, 100):
    my_data2[i,:, :] = mnist_train[i][0][:,0:28,0:28]
print(my_data2.shape)

(100, 28, 28)

在需要获取特定区域的元素时，我们可以使用上面设置起始索引和结束索引的方法，沿着张量每个轴的指定位置来进行区域选择。例如，你可以在所有图像的右上角截取出10像素×10像素的区域：

# 4. 通过指定起始索引和结束索引来导入部分原始张量（10×10）
my_data2 = np.zeros([100, 10, 10])    # 初始化一个与目标尺度相同的张量
for i in range(0, 100):
    my_data2[i,:,:] = mnist_train[i][0][:,18:,0:10]
print(my_data2.shape)

(100, 10, 10)

在以上代码中，我们并没有直接使用更通用的语法 train_images[0:100,:,:] 来实现目标张量的切片。这主要是因为无论是sklearn库还是paddle库，它们所内置的MNIST数据集都没有直接使用4D张量，而是使用序列数据类型来存储样本。在数据集的序列变量中，每个序列的元素都以2D或者3D张量来存储样本，最终，整个序列就构成了完整的数据集。这种保存数据的方式，与我们前面介绍的以4D张量来存储数据并没有太大的区别。但应注意，无论数据源是以什么形态来保存输入样本，在最终输入到深度神经网络的时候，基本都是采用纯粹的张量来进行存储。例如，以4D张量来存储彩色图片。到这里，也许你会感到疑惑，图像不是只有三个维度吗？为什么会使用4D张量来进行存储呢？这就涉及到 2.1.3 小节中我们将要介绍的数据批量的概念。

（3）连接

在进行数据处理时，我们可能会将两个或多个不同的张量进行拼接。例如，在对彩色图像进行图像色度和饱和度调节时，通常会先将彩色图像转换成HSV格式，然后按照亮度、色度、对比度拆分成三个不同的2D张量进行处理，最后再将这三个2D张量拼接成完整的3D张量彩色图。再比如，在进行视频处理时，可能会先将视频按照帧进行拆分，然后再将若干个连续的帧拼接成一个更大的张量一起送入到模型中进行处理。这些应用都涉及到一个很重要的张量操作——连接（joining）。连接操作实现将两个或多个张量按照指定的轴进行连接。下面的代码分别实现上面描述的这两种常见的应用。

图2-8 张量连接

第一种连接方法实现将两个或多个张量按照新的轴进行顺序相连。例如，程序清单 2-11 中的Red, Green, Blue三个张量的初始形状都是（28×28），当我们将它们进行连接之后，原来的三个2D张量就变成了一个3D张量，表示为：$\boldsymbol{A_{3,i,j}}=concate(\boldsymbol{R}_{i,j}, \boldsymbol{G}_{i,j}, \boldsymbol{B}_{i,j})$。该过程也可以理解为将三张纸叠放在一起（如 图 2-8(a)）。

# codes02013_joining_RGB
import numpy as np

Red = np.arange(784).reshape(28, 28)
Green = np.arange(784).reshape(28, 28)
Blue = np.arange(784).reshape(28, 28)
np.stack((Red, Green, Blue), axis=0).shape

(3, 28, 28)

第二种连接方法实现了将两个或多个张量按照已有的某个轴进行顺序相连。例如， 程序清单2-12 中的4D张量slice1和slice2的初始形态都是（10, 3, 28, 28），它们都代表了10张28×28的彩色图片。利用 np.concatenate() 函数，我们实现了将它们组合成一个包含20张28×28的彩色图片张量，表示为：$\boldsymbol{C_{20,i,j}}=concate(\boldsymbol{A}_{10,i,j}, \boldsymbol{B}_{10,i,j})$。这个过程可以理解为将两根短水管拼接成一个长水管（如 图 2-8(b)）。

# codes02014_joining_concatenate_slice
import numpy as np

slice1 = np.random.randn(10, 3, 28, 28)
slice2 = np.random.randn(10, 3, 28, 28)
slice = np.concatenate((slice1, slice2), axis=0)
slice.shape

(20, 3, 28, 28)

（4）换位

张量的 换位（mutating） 操作与矩阵的转置操作比较相似，都起到改变索引访问次序的作用。矩阵的转置是将行和列两个维度进行交换，使得程序在访问矩阵的索引时，由原来的先访问行、后访问列，转变为先访问列、后访问行。对于张量来说，可能会涉及到多个维度的位置交换。例如，在对一个连续的视频帧序列进行处理时，对于尺度为（5, 3, 28, 28）的输入张量 $\boldsymbol{A}$，在经过一系列的神经网络提取特征后，得到一个尺度为（5, 128, 10, 10）的输出张量 $\boldsymbol{B}$。接下来，需要将这个特征送入到循环神经网络中，并对时间轴进行编码。此时，就需要将张量 $\boldsymbol{B}$ 的各个维度进行换位，以得到符合后续模型规范的张量 $\boldsymbol{C}$，其形状为（128, 10, 10, 5）。在进行维度换位时，为了保证数据不发生变换，需要确保除检索顺序发生改变，每个维度内部的元素顺序都不能改变，即：$\boldsymbol{B}_{i, j, k, l} = \boldsymbol{C}_{j, k, l, i}$。在Python中，我们可以使用 transpose() 函数来调整张量各个轴的顺序，参数 axis=(1,2,3,0) 表示新建张量 $\boldsymbol{C}$ 的轴的顺序分别对应于源张量 $\boldsymbol{B}$ 的序号为（1，2，3，0）的轴。

# codes02015_mutating
import numpy as np

B = np.random.randn(5, 128, 10, 10)
C = B.transpose((1,2,3,0))
C.shape

# 特殊的张量换位——矩阵的转置
B = np.random.randn(3, 4)
C = B.transpose((1,0))
C == B.T

(128, 10, 10, 5)

矩阵的转置是一种特殊的张量换位，它只发生于二阶张量，也即只有对矩阵做行和列的交换才称之为转置。矩阵的转置操作交换的是矩阵第0和第1个轴的顺序，它可以表示为 B.transpose((1,0))，这个过程的结果与2D张量的转置操作 $x^T$ 是相同的。 程序清单2-14 展示了这个过程。

# 特殊的张量换位——矩阵的转置
B = np.random.randn(3, 4)
C = B.transpose((1,0))
C == B.T

array([[ True,  True,  True],
       [ True,  True,  True],
       [ True,  True,  True],
       [ True,  True,  True]])

（5）变形

变形（reshaping） 是张量另外一个重要的基本操作，它实现了张量行的数量和列的数量的改变。变形前后，张量元素的总个数和内容都保持不变。以下代码实现了将一个 $3×4$ 的张量变形为一个 $2×6$ 的张量。注意，变形前后的元素总个数都是12，且元素的值没有发生变化。

# codes02016_reshaping
import numpy as np

# 创建一个3行4列的张量
A = np.array([[0,1,2,3],[4,5,6,7],[8,9,10,11]])

(3, 4)

# 将张量变形为4行3列的张量
B = A.reshape((4,3))
print(B)

[[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]]

# 将张量变形为2行6列的张量
C = A.reshape((2,6))
print(C)

[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]]

2.1.3 数据批量

一般来说，深度学习中所使用的数据集都是张量数据，而所有数据张量的第一个轴（第0个轴）默认都是样本轴（或样本维度）。例如，在MNIST数据集的例子中，第一个轴通常代表的就是数字图像的索引。此外，在深度学习中，由于数据集通常都比较大，因此一般不会一次性处理整个数据集，而是将数据集拆分成多个数据批次，每次只处理一个批次的数据，这种方法称之为数据批量。下面，我们使用切片的方法实现将原始的MNIST数据集按照批次大小（BatchSize）为256的标准进行批次划分。注意，此处的代码仅作为对数据张量的批量划分的演示，完整的数据划分，请参考第 4.3 节中的数据读取部分。

首先给出整个MNIST训练集的总样本数，它总共有60000张图片：

# codes02017_data_batches

# 1. 整个数据集的样本数
len(mnist_train)

60000

然后是第一个批量，其样本ID为0~255。

# 2. 第一个批量的样本数
batch = mnist_train.images[:256]
len(batch)

256

接下来是第二个批量的数据，其样本ID为256~511。

# 3. 第二个批量的样本数
batch = mnist_train.images[256:512]
len(batch)

256

最后是第n个批量的数据，其样本ID为 $256n ~ 256(n+1)$

# 4. 第n个批量的样本数
n=10
batch = mnist_train.images[256*n : 256*(n+1)]
len(batch)

256

以上数据划分方法是一种形象化的示例，在传统的机器学习的任务中还是比较常见的。但是在使用深度学习的实际应用中，我们通常会借助于深度学习工具包中预先封装好的批次划分工具来生成批量数据。第 4.3 中，我们给出了基于Paddle的示例。

2.1.4 现实世界中的数据

近年来，深度学习被应用到现实世界的方方面面，但归纳之后你会发现几乎所有实例所使用的数据类型基本上都可以归纳为以下几种。

2.1.4.1 向量数据（2D张量）

向量数据是使用二阶张量进行存储，每条数据都被编码为向量形态的一类数据，其形态为（samples, features）。二阶张量的第一个轴（索引为0的轴）称为样本轴，用于索引样本；第二个轴（索引为1的轴）为特征轴，用来存储样本各个维度的特征。

下面给出几个例子：

• 鸢尾花数据集（iris）： 该数据集由 Edgar Anderson 收集，并由著名的统计学和生物学家 R.A Fisher 于1936年引用来用于线性判别分析。鸢尾花数据集收集了150条不同种类的鸢尾花属性数据，分别是花萼的长、花萼的宽、花瓣的长和花瓣的宽。这些鸢尾花分别属于Setosa、Versicolour和Virginica三个类中的一种，每种包含50条记录。该数据集最终存储在形状为（150, 5）的张量中，示例如下：

• 糖尿病预测数据集（diabetes）： 该数据集总共包含768个样本，每个样本有8种不同的特征。因此，该数据集被保存在形状为（768，8）的张量中。

2.1.4.2 时序数据或序列数据（3D张量）

有些数据在时间维度（序列顺序）上是具有先后顺序的，此时就需要增加一个轴来对时间（序列）进行索引。这类数据通常被编码为一个向量序列，第一个轴（索引为0的轴）依然用来索引样本的样本轴，第二个轴（索引为1的轴）用来索引时间的时间轴，而第三个轴（索引为2的轴）为特征轴，用来存储样本各个维度特征的特征值。因此，一个数据批量最终将被编码为一个三阶张量，其形态为（samples, timesteps, features）（如 图 2-7）。

图2-9 时序数据组成的3D张量

下面给出几个例子：

• 股票价格数据集（stock）：在该数据集中，某天收盘时的3770支股票的基本数据，包括涨跌值、幅度、市盈率、换手率、开盘价、收盘价等17种不同的特征值。此时，整个交易日可以被编码成一个形态为（3770, 17）的2D张量。如果以单支股票为第0号索引，则一年中全部的250个交易日的数据，就可以保存在一个形状为（3770，250，17）的三阶张量中。

• 文本序列数据集：以某社交网络APP为例。某用户一年中共发布了1000篇动态，按照每条动态允许文字上限数1500进行编码，生成由1500个字组成的序列。假设每个字都来自于3500个常用汉字中的一个。在这样的情况下，每个字符可以被编码为7000个字节的二进制向量（注意每个中文字符在计算机中需要使用2个字节进行存储）。那么，该用户一年中所发布的文本动态信息就可以被存储在一个形状为（1000, 1500, 7000）的三阶张量中。此时，文本序列的形状为（样本数，字序号，字编码）

2.1.4.3 图像数据（4D张量）

图像数据具有三个维度，分别是高度（Height）、宽度（Width）和颜色通道（channel）。因此，加上样本轴后，通常使用4D张量来编码图像批量。一般来说，图像张量的形状有两种约定，一种是通道在前（channels_first）模式，又称为 NCHW 模式（samples, channels, height, width）；另一种是通道在后（channels_last）模式，又称为 NHWC 模式（samples, height, width, channels）。这两种约定所存储的数据是完全相同的，但因为顺序的不同会导致数据访问的形式和执行速度存在一定的差异。由于数据读取是按照通道的顺序进行，且对于图像数据来说，每个像素都必须完成所有通道的读取才能进行显示。因此，使用NCHW形态存储的数据，设备需要把所有通道的值都读取完毕才能进行计算；而使用NHWC形态存储的数据每次只需要读取三个像素即可完成彩色像素的计算。相对而言，前者更适于基于具有高带宽和高并行性的GPU设备的运算；后者更适合于具有高频率的CPU设备的运算。目前，大多数深度学习库都同时支持这两种存储模式，但建议在使用GPU进行训练的时候，尽量使用NCHW模式，以加快并行运算的效率；而对于使用CPU进行单样本推理的时候，可以考虑使用NHWC模式。此外，需要注意的是，许多深度学习库默认使用的著名的图像处理库OpenCV，其默认模式为NHWC。图 2-10 分别给出了 NCHW 和 NHWC 两种模式下图像数据的4D张量示意图。

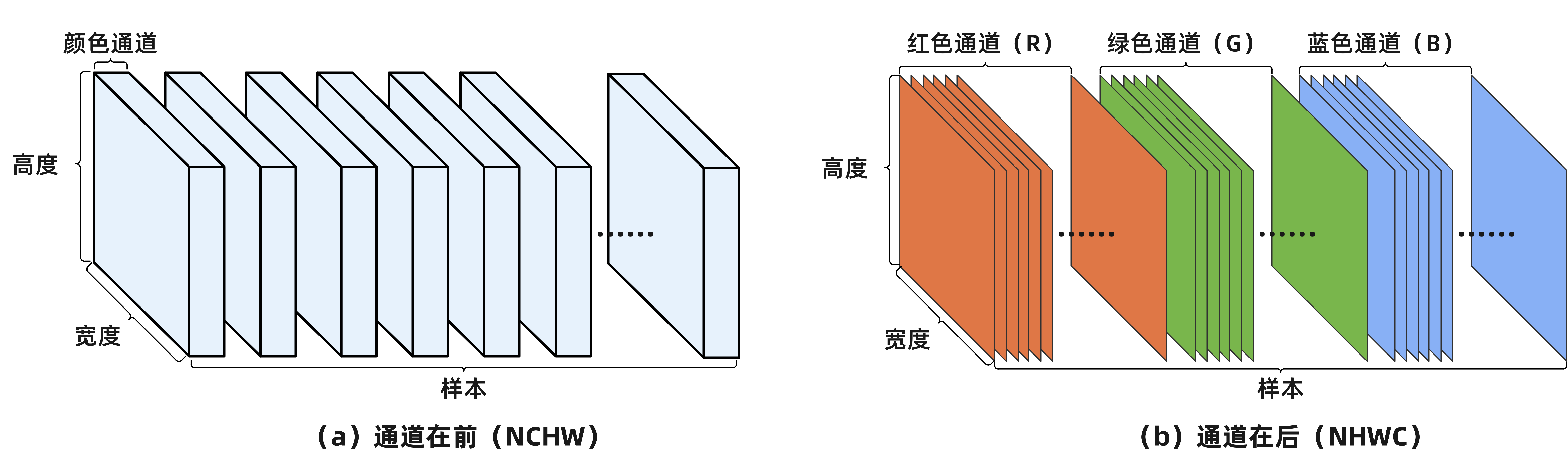
图2-10 图像数据组成的4D张量

此外，虽然灰度图像（例如常见的MNIST数据集）只有一个颜色通道，但为了统一图像的存储和表示方式，按照惯例，依然使用四阶张量来表示图像的批量数据。与彩色图像不同的是，灰度图像的通道值 channels=1，而彩色图像的通道值 channel=3。例如，对于分辨率为800×600的图像，如果批量大小为256，则由灰度图像组成的批量可以保存在一个形状为（256, 1, 600, 800）的张量中，而由彩色图像组成的批量则可以保存在一个形状为（256, 3, 600, 800）的张量中。

2.1.4.4 视频数据（5D张量）

视频数据是现实生活中少数需要使用五阶张量来表示的数据类型之一，更高维度的张量数据在常见的深度学习应用中是罕见的，也超出了本书的讨论范围。因此，视频数据将是我们讨论的最高维度的张量数据。视频可以被看作是一系列帧的组合，每一帧都是一幅彩色图像或者灰度图像。因此，在对视频数据进行存储的时候，我们会在第0号样本轴后面增加一个 时间轴 来索引不同时间点上图像帧数据。与图像数据类似，视频数据通常也有两种约定模式，一种是 NFCHW（samples, frames, channels, height, width），另一种是 NFHWC（samples, frames, height, width, channels）。

举个例子，一个以每秒30帧进行采样的15秒的视频片段，视频尺寸为1080×608，它的总帧数为450帧。如果将100个这样的视频片段组合成一个批量并将其保存在一个张量中，则该张量是一个形态为（100, 450, 608, 1080, 3）的5D张量。粗略算一下，它包含 88,646,400,000 个值，若该张量的数据类型是float32，也即每个值都是32位浮点型数据，那么这个张量将有330GB。好恐怖的量！当然，在现实生活中，你所遇到的视频要比这个值小很多。因为它们并不是以float32格式进行存储，并且它们通常会被使用特殊的算法进行压缩，例如一个同样规模的MP4视频只需要3~4MB的存储空间。

2.1.5 张量运算

正如所有计算机程序都可以简化为二进制输入以及作用在二进制上的逻辑运算（与、或、非等），深度神经网络所学习到变换也都可以简化为数值张量以及作用在张量上的一些 张量运算（tensor operation），例如张量加法、张量乘法和张量变形等。

在第 1.3 小节的初识神经网络中，我们通过堆叠Linear层和ReLU层来构建神经网络。在Paddle中，它们的实例如下所示：

paddle.nn.Linear(in_features=100, out_features=256)
paddle.nn.ReLU()

以上两层可以理解为两个简单函数，它们组合成的复合函数就是神经网络最基本的线性变换。对于这个复合函数，输入是一个2D张量，输出返回的是另一个2D张量，也就是说 Linear+ReLU 实现了输入张量的线性变换。具体而言，该复合函数可以公式化为：

$$\boldsymbol{Y} = relu(\boldsymbol{W} * \boldsymbol{X} + \boldsymbol{b}) \tag{2.12}$$

其中，$\boldsymbol{W}$ 叫权重参数，它是一个2D张量，输入 $\boldsymbol{X}$ 是另一个2D张量，$\boldsymbol{b}$ 称之为偏置，它是一个向量。将该函数拆解开看，它可以理解为三个张量运算的组合。输入张量 $\boldsymbol{X}$ 和权重张量 $\boldsymbol{W}$ 之间的点积（*）运算、得到的积（2D张量）与向量 $\boldsymbol{b}$ 之间的张量加法（+）运算，以及最后的 relu 运算。relu(x) 运算相当于求最大值的 max(x, 0) 运算。

2.1.5.1 逐元素运算

relu运算和张量加法都是典型的 逐元素（element-wise） 的运算，这就意味着执行这类运算的张量中的每个元素都会依据相同的运算规则进行计算。如果你想编写简单的代码来实现两个张量的逐元素运算，那么for循环是比较合适的办法。不过，借助于向量化编程实现，我们可以使用更为简单的办法来实现逐元素运算。在实践中，对于Numpy数组的处理，大多数时候都是基于事先优化好的数学库来实现，例如英特尔数学核心库（MKL, Intel Math Kernel Library）和基础线性代数子程序(BLAS, Basic Linear Algebra Subprograms)。它们都是低层次、高并行、高效的张量操作库，其底层运算都使用C或C++语言来实现，而在高层都提供了Python的封装。借助于C++的高性能特性，这些库比单纯的Python程序要快数倍，但保留了Python代码的易用性和书写便利。

标量、向量、矩阵和张量都有一些实用的属性。例如，在逐元素运算中，任何按元素进行的一元运算都不会改变其操作数的形状；同样，任意给定具有相同形状的两个张量，其运算结果的形状也保持不变。例如，只要形状相同，我们就可以把两个张量进行相加。两个三阶张量相加是将这两个张量所有对应位置的元素进行相加，也即逐元素相加，比如 $\boldsymbol{C}=\boldsymbol{A}+\boldsymbol{B}$，其中 $C_{i,j,k}=A_{i,j,k}+B_{i,j,k}$。再比如，对张量 $\boldsymbol{X}$ 执行relu运算也相当于对 $\boldsymbol{X}$ 的所有元素分别执行relu运算，即：$Y_{i,j,k} = relu(X_{i,j,k})$。下面的代码是这两种运算的Python实现。

# codes02018_element-wise
import numpy as np

# 1. 张量加法
A = np.arange(8).reshape(2, 4)
B = A.copy()
print("A = {}, \n B = {}, \n C = A + B = {}".format(A, B, A+B))

# 2. relu运算
X = np.random.randn(3, 4)
print("X = {}, \n relu(X) = {}".format(X, np.maximum(X, 0)))

A = [[0 1 2 3],
     [4 5 6 7]], 
B = [[0 1 2 3],
     [4 5 6 7]], 
C = A + B = [[ 0  2  4  6],
             [ 8 10 12 14]]

X = [[ 1.61040524  1.16370583 -0.13859777 -2.39714489],
     [ 0.94058832 -1.71012614  1.22631294  0.81664416],
     [-0.22455861 -0.88797895 -1.23648328  0.4056167 ]], 
relu(X) = [[1.61040524 1.16370583 0.         0.        ],
           [0.94058832 0.         1.22631294 0.81664416],
           [0.         0.         0.         0.4056167 ]]

根据同样的运算规则，也可以实现逐元素的乘法、减法等其他基本运算。下面我们再给出一个常用的逐元素运算，即两个矩阵之间的按元素乘法，这种乘法称为 哈达玛乘积（Hadamard product）。在代数系统中，Hadamard乘积使用符号 $\odot$ 表示。给定矩阵 $\boldsymbol{A} \in \mathbb{R}^{m×n}$ 和矩阵 $\boldsymbol{B} \in \mathbb{R}^{m×n}$，若它们的第i行和第j列的元素分别是 $a_{ij}$ 和 $b_{ij}$，则矩阵 $\boldsymbol{A}$ 和矩阵 $\boldsymbol{B}$ 的Hadamard乘积等于：

$$C = \boldsymbol{A} \odot \boldsymbol{B} = \begin{bmatrix} a_{11} b_{11} & a_{12} b_{12} & \cdots & a_{1n} b_{1n} \\ a_{21} b_{21} & a_{22} b_{22} & \cdots & a_{2n} b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} b_{m1} & a_{m2} b_{m2} & \cdots & a_{mn} b_{mn} \\ \end{bmatrix} \tag{2.13}$$

# codes02026_multiply_hadamard
A = np.arange(16).reshape((4,4))
B = A.copy()
print('A={},\nB={}'.format(A, A*B))

A=[[ 0  1  2  3]
   [ 4  5  6  7]
   [ 8  9 10 11]
   [12 13 14 15]],
B=[[  0   1   4   9]
   [ 16  25  36  49]
   [ 64  81 100 121]
   [144 169 196 225]]

2.1.5.2 广播

在上一小节张量加法的简单实现中，我们发现加法运算的两个张量必须满足 形状相同 这个前置条件。那么，如果将两个形状不同的张量进行相加，会发生什么呢？在深度学习中，我们会使用一些不那么常规的规则来扩展线性代数的基本运算规则。例如，我们允许将矩阵和向量相加，产生另外一个矩阵：$\boldsymbol{C}=\boldsymbol{A}+\boldsymbol{b}$，其中 $C_{i,j} = A_{i,j} + b_j$。也就是说，矩阵 $\boldsymbol{A}$ 的每一行都会与向量 $\boldsymbol{b}$ 进行相加。这种方式允许我们不需要在进行矩阵和向量加法运算时，事先将向量 $\boldsymbol{b}$ 复制扩展成与矩阵 $\boldsymbol{A}$ 相同形状的矩阵。这种隐式地复制向量 $\boldsymbol{b}$ 到很多位置以匹配大张量形状的方法，称为 广播（broadcast）。

从上面的描述，我们可以知道广播主要包含两个步骤：
（1）对齐已经存在的轴，然后向较小的张量添加一个 广播轴，使其维度与较大张量的维度相同；
（2）将新生成的张量沿着广播轴复制向量，使其最终形状与较大张量相同。

# codes02019_broadcast
import numpy as np

# 1. 从向量到二阶张量的广播
A1 = np.arange(24).reshape(3, 8)    # 构建一个形状为3×8的二阶张量 
b1 = np.ones([1,8])*0.5             # 构建一个形状为1×8的向量
print('A1 = {}, \n A1+b1 = {}'.format(A1, A1+b1))

# 2. 从标量到三阶张量的广播
A2 = np.arange(12).reshape(2,2,3)   # 构建一个形状为2×3×4的三阶张量
b2 = 0.5                            # 构建一个形状为1×1的标量
print('A2 = {}, \n A2+b2 = {}'.format(A2, A2+b2))

A1    = [[ 0  1  2  3  4  5  6  7]
         [ 8  9 10 11 12 13 14 15]
         [16 17 18 19 20 21 22 23]], 
A1+b1 = [[ 0.5  1.5  2.5  3.5  4.5  5.5  6.5  7.5]
         [ 8.5  9.5 10.5 11.5 12.5 13.5 14.5 15.5]
         [16.5 17.5 18.5 19.5 20.5 21.5 22.5 23.5]]

A2    = [[[ 0  1  2]
          [ 3  4  5]]
         [[ 6  7  8]
          [ 9 10 11]]], 
A2+b2 = [[[ 0.5  1.5  2.5]
          [ 3.5  4.5  5.5]]
         [[ 6.5  7.5  8.5]
          [ 9.5 10.5 11.5]]]

2.1.5.3 求和运算

另一种有用的操作是对张量的元素进行求和。在张量运算中，由于存在多维度信息，因此也存在多种不同类型的求和操作，下面我们简单介绍一下这些不同类型的求和操作。

1. 对所有元素求和

在数学表示法中，我们使用符号 $\sum$ 表示求和。因此，我们可以使用公式 $\sum^d_{i=1} x_i$ 来表示长度为d的向量中的所有元素的总和。在代码中可以直接调用numpy的 sum() 函数来实现这个功能。

# codes02020_sum_element_vector
A = np.arange(5)
print('A = {}, \nA_sum = {}'.format(A, A.sum()))

A     = [0 1 2 3 4], 
A_sum = 10

向量求和是最简单的按元素求和，我们也可以使用类似的方法对任意形状的张量进行按元素求和。例如，对三阶张量 $\boldsymbol{B_{(l,m,n)}}$ 进行按元素求和，可以记作：$\sum^l_{i=1}\sum^m_{j=1}\sum^n_{k=1} b_{ijk}$。

# codes02021_sum_element_3DTensor
B = np.ones([2,3,4])
print('B = {}, \nB_sum = {}'.format(B, B.sum()))

B     = ([[[1., 1., 1., 1.], [1., 1., 1., 1.], [1., 1., 1., 1.]],
          [[1., 1., 1., 1.], [1., 1., 1., 1.], [1., 1., 1., 1.]]]),
B_sum = 24.0

2. 按轴降维求和

正如上面的两个例子所示，默认情况下，求和函数 sum() 会沿着张量所有轴来顺序求取所有元素的和，使张量最终变成一个标量。然而，我们并不总是期望它这么做。有时候，我们期望它能够沿着某个指定的轴来进行求和。以下面的矩阵为例，已知语文、数学、英语和信息技术四门课的成绩，我们希望能够通过按行求和来获得每个同学的总成绩，而不是一次性计算所有人、所有科目的成绩总和。

此时，我们可以通过指定函数的轴序号，来实现按轴计算。例如，当我们设置 axis=1 时，输入矩阵将沿着 1 轴进行列降维求和并产生向量，最终输入轴 1 的维数在输出形状中将会消失。因此，这种按轴求和的方法，称为 降维求和。

# codes02022_sum_axis
import numpy as np

# 0. 定义一个3行、4列的张量
A = np.array([[87,90,88,70],[67,79,96,80],[90,90,95,97]])
A, A.shape

(array([[87, 90, 88, 70],
        [67, 79, 96, 80],
        [90, 90, 95, 97]]),
 (3, 4))

# 1. 按照 axis=1 轴进行降维求和
A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape

(array([335, 322, 372]), (3,))

相似地，如果我们指定 axis=0，则矩阵会按照行进 行 降维求和。与此同时，输入轴 0 的位数也将在输出形状中消失。

# 2. 按照 axis=0 轴进行降维求和
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape

(array([244, 259, 279, 247]), (4,))

如果同时沿着 行 和 列 对矩阵求和，则等价于对矩阵中的所有元素进行求和。相似地，对于一个n阶张量，如果同时沿着所有维度进行张量求和，则等价于对该张量的所有元素进行求和。

# 3. 同时按照 axis=0, axis=1 轴进行降维求和
A_sum_axis01 = A.sum(axis=(0,1))
A_sum_axis01

1029

一个与求和相关的计算是求 平均值（mean或average）。在Python中，我们可以调用函数 mean() 来计算任意形状张量的平均值。与求和类似，计算平均值时也可以沿着指定轴来降低张量的维度。

# 4. 按照 axis=0 轴进行降维求平均值
A_mean_axis0 = A.mean(axis=0)
A_mean_axis0, A_sum_axis0.shape

(array([81.33333333, 86.33333333, 93.        , 82.33333333]), (4,))

3. 非降维求和

有趣的是，在上面的例子中，无论按照哪个轴进行求和或求平均值，最终的输出都会变成一个向量。但是有时候，我们又希望在计算总和或均值时保持轴数不变。比如，我们想要计算矩阵 $\boldsymbol{A}$ 中的每个元素占 $\boldsymbol{A}$ 的元素和的比例。在Numpy中，我们只需要设置参数 keepdims=True 就可以实现这个功能。这种求和运算后仍然能保持张量维度不变的求和运算称之为 非降维求和。如下面的代码所示，依然是按照 axis=1 进行求和，但最终的输出却保持了张量原来的阶数，依然是一个2D张量。

# 5. 按照 axis=1 轴进行非降维求和
A_sum2 = A.sum(axis=1, keepdims=True)
A_sum2, A_sum2.shape

(array([[335],
        [322],
        [372]]),
 (3, 1))

此时，如果我们以原始的2D张量 $\boldsymbol{A}$ 去除以非降维求和后的汇总值 $\boldsymbol{A}_{sum2}$ ，将得到 $\boldsymbol{A}$ 中的每一项占 $\boldsymbol{A}_{sum2}$ 的比例。换句话说，由于汇总值在对每一行求和后，仍然保持两个轴不变，所以可以直接通过广播的方法将 $\boldsymbol{A}_{sum2}$ 的维度统一到和 $\boldsymbol{A}$ 一致，从而方便进行按元素的除法运算。

# 6. 求单个元素占汇总值的比例
A/A_sum2

array([[0.25970149, 0.26865672, 0.26268657, 0.20895522],
       [0.20807453, 0.24534161, 0.29813665, 0.2484472 ],
       [0.24193548, 0.24193548, 0.25537634, 0.26075269]])

4. 累积求和

最后还有一种常见的求和方法，称为 累积求和。如下列代码所示，它实现了矩阵沿着某个轴计算张量 $\boldsymbol{A}$ 各元素的累积总和。值得注意的是，累积求和通常需要事先指定轴来进行运算。否则，计算可能会因为跨行或跨列导致跨样本或者跨特征累积。这种情况通常没有太多实际的意义。

# 7. 累积求和
A.cumsum(axis=1)

array([[ 87, 177, 265, 335],
       [ 67, 146, 242, 322],
       [ 90, 180, 275, 372]])

2.1.5.4 张量乘法

前面我们已经学习了逐元素运算、广播运算以及求和运算，另外一个重要的运算是张量乘法。下面我们将分别介绍人工智能算法中最常用的三种张量乘法运算，它们分别是：向量与向量间的乘法、矩阵与向量间的乘法、矩阵与矩阵间的乘法。

1. 向量与向量间的乘法

给定两个向量 $\boldsymbol{x},\boldsymbol{y} \in \mathbb{R}^n$，它们之间的乘积 $\boldsymbol{x}^T\boldsymbol{y}$ （或 $<\boldsymbol{x}, \boldsymbol{y}>$）是一个实数。这个实数 $\boldsymbol{z}$ 称为向量 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 的 点积 (dot product) 或 内积(inner product)。点积运算等价于两个向量 $\boldsymbol{x},\boldsymbol{y}$ 相同位置的按元素乘积的和，可以表示为：

$$\boldsymbol{z}=\boldsymbol{x}^T\boldsymbol{y} =\sum^n_{i=1} x_i y_i \tag{2.14}$$

值得注意的是，对于向量 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ ，总是存在 $\boldsymbol{x}^T\boldsymbol{y} = \boldsymbol{y}^T\boldsymbol{x}$。

以上过程可以用如下代码表示：

# codes02023_multiply_vector_by_vector
import numpy as np
# 1. 使用点积计算两个向量间的乘法
x = np.array([1,2,3,4,5])
y = np.ones(5)
print('x和y的点积为：{}'.format(np.dot(x,y)))

x和y的点积为：15.0

如果执行按元素乘法，然后再求和来表示两个向量的点积，则表示为：

# 2. 使用逐元素乘法+求和计算两个向量间的乘法
print('x和y的逐元素乘积的和为：{}'.format(np.sum(x*y)))

x和y的逐元素乘积的和为：15.0

若给定向量 $\boldsymbol{x} \in \mathbb{R}^m, \boldsymbol{y} \in R^n$，则 $\boldsymbol{x} \times \boldsymbol{y}$ 被称为向量 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 的外积（或向量积、叉乘）。此时，乘法运算的结果不再是一个实数，而是一个矩阵，可以表示为：$\boldsymbol{Z}=(\boldsymbol{x}\boldsymbol{y}^T)_{ij}=x_i y_j$，也就是说：

$$\begin{equation} z=\boldsymbol{x}\boldsymbol{y}^T \in \mathbb{R}^{m×n} = \begin{bmatrix} x_{1} y_{1} & x_{1} y_{2} & \cdots & x_{1} y_{n} \\ x_{2} y_{1} & x_{2} y_{2} & \cdots & x_{2} y_{n} \\ \vdots & \vdots & \ddots & \vdots \\ x_{m} y_{1} & x_{m} y_{2} & \cdots & x_{m} y_{n} \\ \end{bmatrix} \tag{2.15} \end{equation}$$

一般来说，在大多数的应用中，点积的作用要远远高于外积。在很多机器学习的场景中都会应用到点积。例如，在前面介绍的神经网络最基本的形式 $\boldsymbol{y}=\boldsymbol{w}\boldsymbol{x}+b$ 中。若存在一组由向量 $\boldsymbol{x} \in \mathbb{R}$ 表示的输入，和一组由向量 $\boldsymbol{w} \in \mathbb{R}$ 表示的权重，那么输入 $\boldsymbol{x}$ 关于权重 $\boldsymbol{w}$ 的加权和可以表示为 $\boldsymbol{x}^T \boldsymbol{w}$。当权重为非负数，且 $\sum^n_{i=1}w_i = 1$ 时，点积就是两个向量的加权平均值（weighted average）。在几何表示法中，如果将这两个向量规范化到单位长度，点积则表示它们夹角的余弦。

2. 矩阵与向量间的乘法

有了向量间点积的概念，让我们再来理解一下 矩阵-向量积（matrix-vector product）。给定如 公式 2.5 的矩阵 $\boldsymbol{A} \in \mathbb{R}^{m×n}$ 和如 公式 2.3 所示的列向量 $\boldsymbol{x} \in \mathbb{R}^m$，我们可以得到它们之间的乘积 $\boldsymbol{y}$。不难验证，$\boldsymbol{y}$ 是一个向量。下面我们将使用两种方法来解释矩阵和向量之间的乘法运算。

首先，假设我们将矩阵 $\boldsymbol{A}$ 用逐行的形式表示，那么我们可以将 $\boldsymbol{A}\boldsymbol{x}$ 表示为：

$$\boldsymbol{y}=\boldsymbol{A}\boldsymbol{x} = \begin{bmatrix} — & \boldsymbol{a^T_1} & — \\ — & \boldsymbol{a^T_2} & — \\ — & \vdots & — \\ — & \boldsymbol{a^T_m} & — \\ \end{bmatrix}\boldsymbol{x} = \begin{bmatrix} \boldsymbol{a^T_1}\boldsymbol{x} \\ \boldsymbol{a^T_2}\boldsymbol{x} \\ \vdots \\ \boldsymbol{a^T_m}\boldsymbol{x} \\ \end{bmatrix}. \tag{2.16}$$

换句话说，乘积 $\boldsymbol{y}$ 的第 $i$ 项等于矩阵 $\boldsymbol{A}$ 的第 $i$ 行与向量 $\boldsymbol{x}$ 的内积，即：$\boldsymbol{y_i}=\boldsymbol{a^T_i} \boldsymbol{x}$。

如果我们将矩阵 $\boldsymbol{A}$ 用列向量的形式写出时，我们可以将 $\boldsymbol{A}\boldsymbol{x}$ 表示为：

$$y=\boldsymbol{A}\boldsymbol{x} = \begin{bmatrix} \mid & \mid & \mid & \mid \\ \boldsymbol{a_1} & \boldsymbol{a_2} & \cdots & \boldsymbol{a_n} \\ \mid & \mid & \mid & \mid \\ \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{bmatrix} = \boldsymbol{a_1}x_1 + \boldsymbol{a_2}x_2 + \cdots + \boldsymbol{a_n}x_n . \tag{2.17}$$

换句话说，$\boldsymbol{y}$ 是一个关于矩阵 $\boldsymbol{A}$ 的列的线性组合(linear combination)，其系数为 $\boldsymbol{x}$。从某种角度上来说，我们可以将矩阵 $\boldsymbol{A} \in \mathbb{R}^{m×n}$ 看作是一个 $n$ 维向量向 $m$ 维向量转换的变换矩阵。这种转换是非常有用的，在多层感知机MLP中，假设第L层的输入是一个 $n$ 维的向量，我们只需要使用一个 $m×n$ 维的权重矩阵就可以实现将输入转换为 $m$ 维度的输出向量，从而轻松地实现升维或降维。正如前面 公式 2.12 所描述的，$\boldsymbol{Y} = relu(\boldsymbol{W} * \boldsymbol{X} + \boldsymbol{b})$。

在代码中使用张量来表示矩阵-向量积时，我们依然可以使用 np.dot() 函数来实现。需要注意的是，矩阵 $\boldsymbol{A}$ 的列的维数必须与向量 $\boldsymbol{x}$ 的维数（长度）保持一致。

# codes02024_multiply_matrix_by_vector
A = np.array([[1,2,3,4,5],[2,3,4,5,6],[3,4,5,6,7]])
x = np.ones(5)
print(A.shape, x.shape, np.dot(A,y))

(3, 5) (5,) [15. 20. 25.]

以上给出了用一个列向量对矩阵 $\boldsymbol{A}$ 进行右乘的形式，我们也可以使用一个行向量对矩阵 $\boldsymbol{A}$ 进行左乘运算。该运算可以公式化为：$\boldsymbol{y}^T=\boldsymbol{x}^T \boldsymbol{A}$，其中 $\boldsymbol{A} \in \mathbb{R}^{m×n}, x \in \mathbb{R}^m, \boldsymbol{y} \in \mathbb{R}^n$。和前面一样，我们可以根据矩阵 $\boldsymbol{A}$ 是行向量或列向量的形式，将乘积 $y^T$ 用两种方式来表示。首先，我们将矩阵 $\boldsymbol{A}$ 表示为列向量的形式，则有：

$$\boldsymbol{y}^T = \boldsymbol{x}^T \boldsymbol{A} = \boldsymbol{x}^T \begin{bmatrix} \mid & \mid & \mid & \mid \\ \boldsymbol{a_1} & \boldsymbol{a_2} & \cdots & \boldsymbol{a_n} \\ \mid & \mid & \mid & \mid \\ \end{bmatrix} = [\boldsymbol{x}^T \boldsymbol{a_1} \quad \boldsymbol{x}^T \boldsymbol{a_2} \quad \cdots \quad \boldsymbol{x}^T \boldsymbol{a_n}]. \tag{2.18}$$

也就是说，$\boldsymbol{y}^T$ 的第 $i$ 项等于向量 $\boldsymbol{x}$ 和矩阵 $\boldsymbol{A}$ 第 $i$ 列之间的内积，$\boldsymbol{y}^T_i = \boldsymbol{x}^T \boldsymbol{a_i}$。

最后，当我们用行向量的形式表示矩阵 $\boldsymbol{A}$ 时，我们可以将 $\boldsymbol{y}^T$ 表示为：

$$\boldsymbol{y}^T = \boldsymbol{x}^T \boldsymbol{A} = [x_1 x_2 \cdots x_n] \begin{bmatrix} — & \boldsymbol{a}^T_{1} & — \\ — & \boldsymbol{a}^T_{2} & — \\ — & \vdots & — \\ — & \boldsymbol{a}^T_{n} & — \\ \end{bmatrix} = x_1 \boldsymbol{a}^T_{1} + x_2 \boldsymbol{a}^T_{2} + \cdots + x_n \boldsymbol{a}^T_{n}. \tag{2.19}$$

我们可以发现此处也是一个关于矩阵 $\boldsymbol{A}$ 所有行的线性组合，它的系数为向量 $\boldsymbol{x}$。不过值得注意的是，在机器学习中，使用列向量对矩阵进行右乘会比使用行向量对矩阵进行左乘更加常用一些。

3. 矩阵与矩阵间的乘法

矩阵与矩阵间的乘法(matrix product) 是张量最重要的运算。如果矩阵 $\boldsymbol{A}$ 和矩阵 $\boldsymbol{B}$ 可以执行乘法运算，那么它们的乘积也必然为矩阵。为了使矩阵乘法能够成立，矩阵 $\boldsymbol{A}$ 的行数必须和矩阵 $\boldsymbol{B}$ 的列数相等。假设存在矩阵 $\boldsymbol{A} \in \mathbb{R}^{m×n}$ 是一个 $m×n$ 的矩阵，矩阵 $\boldsymbol{B} \in \mathbb{R}^{n×p}$ 是一个 $n×p$ 的矩阵。那么它们的乘积将产生一个新的矩阵 $\boldsymbol{C} \in \mathbb{R}^{m×p}$，新矩阵 $\boldsymbol{C}$ 的行数为 $m$，列数为 $p$。我们可以用下面的方式来书写矩阵的乘法：

$$\boldsymbol{C} = \boldsymbol{AB} \in \mathbb{R}^{m×p} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix} \begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1n} \\ b_{21} & b_{22} & \cdots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \cdots & b_{mn} \\ \end{bmatrix} \tag{2.20}$$