【项目030】深度学习的优化（Optimizaiton）方法简介 返回首页

作者：欧新宇（Xinyu OU）
当前版本：Release v0.9
开发平台：Paddle 2.1
运行环境：Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案所涉及的数据集仅用于教学和交流使用，请勿用作商用。

最后更新：2022年1月3日

---

几乎所有的深度学习算法都涉及到优化，与传统机器学习算法在求解优化问题时使用解析法去求解算法设计的优化问题不同；在深度学习中，特别是神经网络的训练过程中，由于庞大的参数数量，使得传统的解析法几乎无法完成这项工作。在神经网络刚刚开始流行的时候，使用几百台机器投入几天甚至几个月来解决单个神经网络的训练问题，是很常见的。随着，任务复杂性的提升以及人们对精度的要求越来越高，优化的代价变得越来越来越让人无法接受。因此，研究人员们开发了一系列专门用于深度学习的优化算法。

这篇教案主要关注的就是面向深度学习的优化问题，即寻找神经网络上的一组参数 $\theta$，使得它能够显著地降低代价函数 $J(\theta)$，该代价函数通常包括整个训练集上的性能评估和额外的正则化项。首先，我们简要介绍导致神经网络优化困难的几个具体挑战；其次，我们会介绍几个具体的优化算法和参数初始化策略；随后，我们将引入更为高级的能够在训练中自适应调整学习率的优化算法；之后，几种常见的学习率衰减策略将被给出；最后，我们会引入百度的Paddle工具包，看看如何在Paddle中实现多学习率的快速配置和实现。

1. 神经网络优化中的挑战问题

---

优化通常是极其困难的任务。在传统机器学习算法中，通常会精心地设计一个目标函数和其约束条件，从而确保优化问题是凸的，以避免一般优化的复杂性。但是，在训练神经网络时，由于深度嵌套，模型通常都是非凸的，即使是凸优化，也并非没有问题。在本节中，我们将总结几个训练深度模型时会涉及的主要挑战。

1.1 病态

1.2 局部最小值

提前遇到局部最小值从而卡住，再也找不到全局最小值了。

1.3 高原、鞍点和其他平坦区域

遇到极为平坦的地方：“平原”，在这里梯度极小，经过多次迭代也无法离开。同理，鞍点也是一样的，在鞍点处，各方向的梯度极小，尽管沿着某一个方向稍微走一下就能离开。

1.4 悬崖和梯度爆炸

"悬崖"，某个方向上参数的梯度可能突然变得奇大无比，在这个地方，梯度可能会造成难以预估的后果，可能让已经收敛的参数突然跑到极远地方去。

1.5 长期依赖

1.6 非精确梯度

1.7 局部和全局结构间的弱对应

1.8 优化的理论限制

2. 基本优化算法

---

为了可视化并更好地理解这些优化算法，我们首先拼出了一个很复杂的一维函数，该函数既包含悬崖又具备局部大量的局部最优，能较好地模拟深度学习中遇到的一些困难。同时，我们也给出该函数的导数形式，并使用几种常见的优化算法，对该函数进行优化。

• 原始函数

$f(x)=2x^3+(0.15x)^2+cos(x)+sin(3x)/3+cos(5x)/5+sin(7x)/7$

• 函数的导数

$f'(x)=6x^2+0.045x-sin(x)+cos(3x)-sin(5x)+cos(7x)$

import os
import numpy as np
import matplotlib.pyplot as plt

def f(x):
    return (0.15*x)**2 + np.cos(x) + np.sin(3*x)/3 + np.cos(5*x)/5 + np.sin(7*x)/7

def df(x):
    return 0.045*x - np.sin(x) -np.sin(5*x) + np.cos(3*x) + np.cos(7*x)

points_x = np.linspace(-20, 20, 1000)
points_y = f(points_x)

plt.plot(points_x, points_y)

[<matplotlib.lines.Line2D at 0x1fdfd687ca0>]

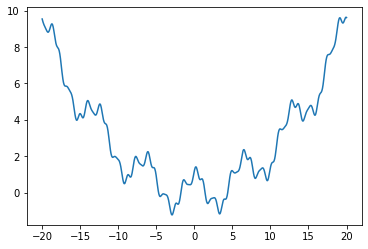
从上图可以看出，该函数既有悬崖，又有大量的局部最小值，说明该函数已经足够复杂。

2.1 随机梯度下降算法 (SGD)

2.1.1 随机梯度下降简介

随机梯度下降（SGD）及其变种是机器学习应用最多的优化算法，特别是在深度学习中。SGD按照数据生成分布随机抽取 m 个小批量样本（独立同分布），通过计算他们的梯度值均值，可以得到梯度的无偏估计。算法H4.1 展示了梯度是如何进行下降的。

学习率是随机梯度下降算法的关键参数。一般来说我们可以使用一个固定的值来作为学习率，例如0.001。但在实践中，有必要随着时间的推移逐渐降低学习率，因此我们将第k步迭代的学习率记作 $\epsilon_k$。与机器学习中面向较小数据集所使用的批量梯度下降算法不同，在SGD中梯度估计引入的噪声源（m个训练样本的随机采样）并不会在极小点处消失；而使用批量梯度下降到达极小点时，整个代价函数的真是梯度会变得很小，接近于0。因此，批量梯度下降可以使用固定的学习率。

实践中，一般会线性衰减学习率直到第 $\tau$ 次迭代：
$$\epsilon_k = (1-\alpha)\epsilon_0 + \alpha \epsilon_{\tau}$$
其中，$\alpha = k / \tau$。在 $\tau$ 步之后，一般使 $\epsilon$ 保持常数。

学习率可以通过实验和误差来选取，通常最好的选择方法是通过检测训练过程中目标函数值随时间变化的学习曲线。当一段时间，验证集损失不再下降时，通常需要进行学习率的衰减操作。这与其说是科学，不如说是一门艺术。我们应该谨慎第参考关于这个问题的大部分指导。使用线性策略时，需要选择的超参数包括 $\epsilon_0, \epsilon_{\tau}, \tau$。通常 $\tau$ 被设定为需要反复遍历训练集数百次的迭代次数，这个次数如前所述需要通过检测验证损失来确定。超参数 $\epsilon_{\tau}$ 应设为大约 $\epsilon_0$ 的1%。因此，主要问题就变成如何设置 $\epsilon_0$。

若 $\epsilon_0$ 太大，学习曲线将会剧烈振荡，损失函数的值通常会明显增加。温和的振荡是良好的，容易在训练随机损失函数（例如增加了Dropout的网络模型）时出现。如果学习率太小，那么学习过程会很缓慢，特别是当初始学习率如果过小，那么学习可能会卡在一个相当高的损失值而保持不变。通常，就总的训练时间和最终损失值而言，最优初始学习率会高于大概迭代数百次后达到最佳效果时的学习率。因此，通常最好是检测最早的几轮迭代，选择一个比在效果上表现最佳的学习率更大的学习率，但不能太大导致严重的振荡。

SGD及相关的小批量（mini-batch）亦或是更广义的梯度优化学习算法，一个重要的性质是每一步更新的计算时间不依赖于训练样本数目的多寡。即使训练样本数目非常大时，它们也能够收敛。对于足够大的数据集，SGD可能会在处理整个训练集之前就收敛到最终测试集误差的某个固定容差范围内。

更多有关SGD的信息，请查看 Bottou (1998)。

2.1.2 随机梯度下降的Python描述

上述的算法可以用下面的公式进行表示，然后改写为python代码

while True：
    x = x - lr*df/dx

def draw_SGD(): 
    model_name = 'SGD'
    save_path = './Handout04Optimization'
    if not os.path.exists(save_path):
        os.mkdir(save_path)    
   
    plt.figure(figsize=(18, 12))     # 生成画布
    for i in range(9):
        plt.subplot(3,3,i+1)
        # 绘制原来的函数
        plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-")
        # 算法开始
        lr = pow(2, -i)*16
        x = -20.0
        GD_x, GD_y = [], []
        for it in range(1000):
            GD_x.append(x), GD_y.append(f(x))
            dx = df(x)
            x = x - lr * dx

        plt.xlim(-20, 20)
        plt.ylim(-2, 10)
        plt.title('SGD, lr={:.4f}'.format(lr))
        plt.plot(GD_x, GD_y, c="r", linestyle="-")
    plt.savefig(os.path.join(save_path, model_name + ".png" ))
    
draw_SGD()

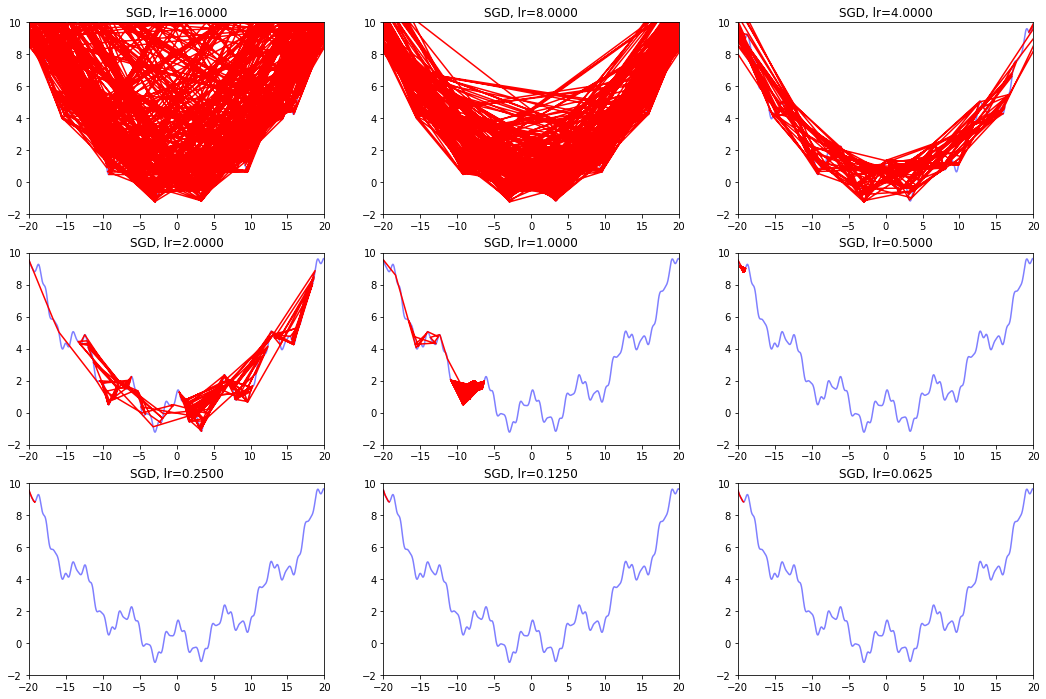
2.1.3 随机梯度下降的Paddle描述

# python 1.8
import paddle.fluid.optimizer as optimizer
opt = optimizer.SGDOptimizer(learning_rate=lr, parameter_list=model.parameters())

# python 2.0
import paddle.optimizer as optimizer
opt = optimizer.SGD(learning_rate=lr, parameters=model.parameters())

2.2 带动量的随机梯度下降 (SGDMomentum)

虽然随机梯度下降仍然是非常受欢迎的优化算法，但其学习过程有时会很慢。带动量的随机梯度下降算法是对随机梯度下降算法的一种改良版本，通常来说优化效果要优于不带动量的随机梯度下降算法。在了解带动量的随机梯度下降算法的基本原理前，我们先看随机梯度下降算法的不足之处。

梯度下降算法根据所使用数据的数据量，可以分为批量梯度下降算法和小批量梯度下降算法。批量梯度下降算法每次都会遍历整个数据集来进行计算，这种方法的优点是优化的过程比较稳定，模型会按照所有样本的整体情况进行优化。早期的机器学习算法由于处理的数据并不是特别多，批量梯度下降算法经常被作为标准优化算法所使用。随着大数据时代的到来，实际应用的数据量通常非常庞大，上百万的训练数据是非常常见的。然而，如果每次执行梯度下降算法时都要求遍历整个训练数据集，将会耗费大量的计算机资源（显存、内存等），这是不可行的。因为拥有数百G甚至数个T显存的GPU并没有出现，即使多卡并行也无法满足如此庞大的要求。在大数据环境中，小批量（mini-batch）梯度下降算法被提出。它的思想非常简单，算法将训练样本分成多个mini-batch，每次迭代训练的时候，送入模型的数据仅仅是一个mini-batch的训练数据，而非整个训练集。例如，对于一个拥有100万训练数据的数据集，我们可以将它分割为10000个mini-batch，每个mini-batch包含100个样本。在训练的时候，每次迭代随机选择一个mini-batch送入模型进行训练，即每次训练只是针对100个样本进行；当10000个mini-batch都完成了一轮训练，我称为完成了一个周期（epoch）的训练。实际应用中，我们发现使用mini-batch的梯度下降算法可以有效地加快训练速度，即提高收敛速度。

在深度学习时代，通常我们所说的随机梯度下降算法（SGD）都是基于小批量数据的随机梯度下降算法（mini-batch SGD），这种算法有效地解决了同时训练的数据过多而导致的设备资源不够的问题，但mini-batch SGD会产生梯度下降过程中上下振荡的现象，使得训练过程不够稳定，容易陷入局部最优问题。（在传统机器学习算法中，我们所说的随机梯度下降，每次仅随机选择1个样本进行训练和梯度优化，与深度学习中的mini-batch SGD略有区别。）

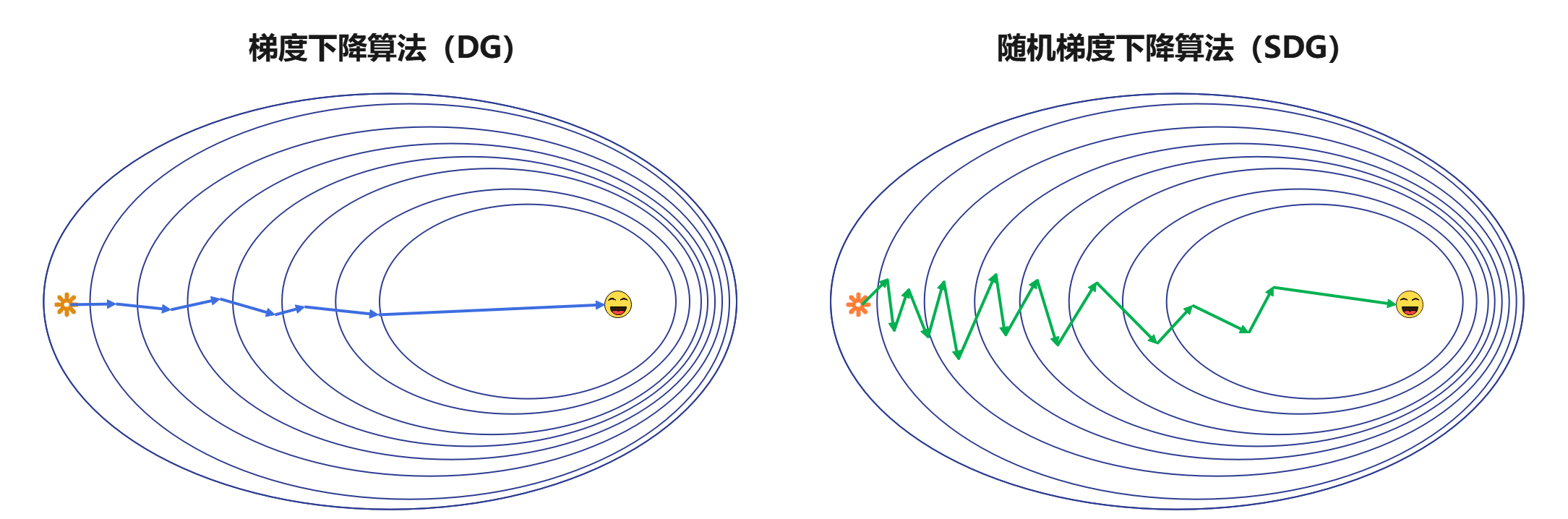
在mini-batch梯度下降算法中，由于每次仅使用数据集中的一部分进行梯度下降，即使mini-batch是进行随机划分，也不可能做到每个mini-batch和完整的训练集完全的独立同分布。因此，每次梯度的下降并不是严格朝最小方向下降，但是总体的下降趋势是朝着最小的方向。从上图中，可以明显看出梯度下降和mini-batch梯度下降的区别。

2.2.1 带动量的随机梯度下降算法简介

为了进一步优化随机梯度下降算法振荡严重的问题，一些研究者提出了基于指数加权平均的梯度下降方法，这其中最优秀的是基于动量（Polyak, 1964）的随机梯度下降算法（SGDMomentum）。动量方法旨在加速学习，特别是处理高曲率、小但一致的速度，或是带噪声的梯度。动量算法积累了之前梯度指数级衰减的移动平均，并且继续沿该方向移动。动量的效果图如下所示：

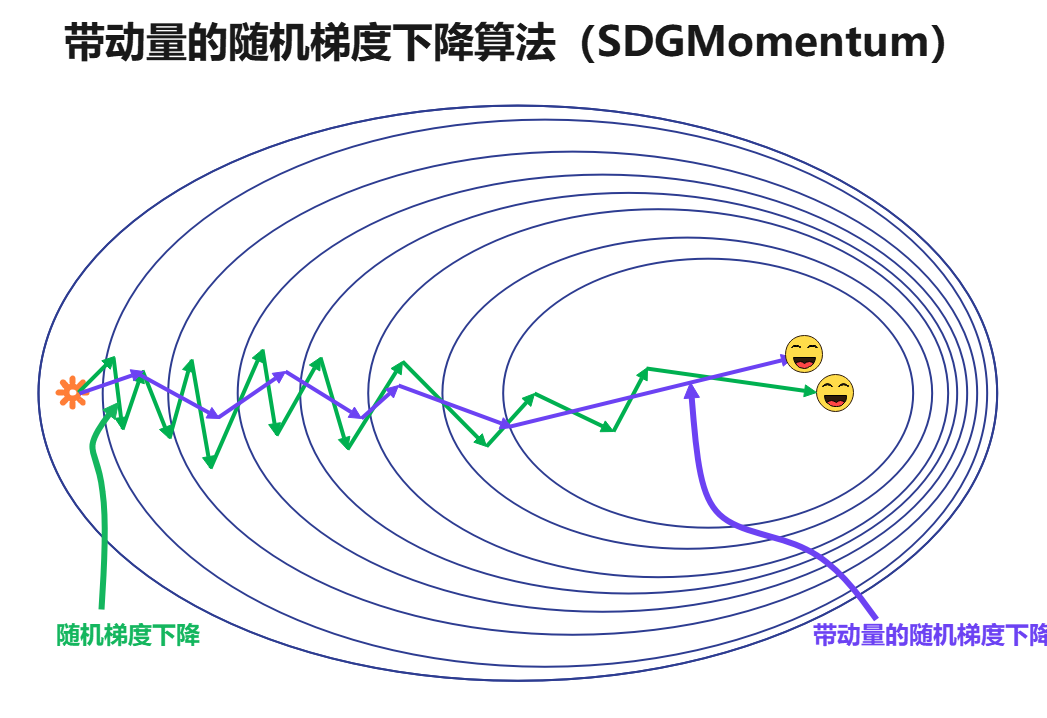
不难发现，经过动量优化之后的SGD，振荡明显减弱了，并且使用更少的周期就可以完成优化。值得注意的是，动量梯度下降算法对于批量梯度下降算法基本无效，它是针对mini-batch梯度下降算法的一种优化。

从形式上看，动量算法引入了变量 $v$ 充当速度的角色————它代表参数在参数空间移动的方向和速率。速度被设置为负梯度的指数衰减平均。名称动量（momentum）来源物理学的类比，根据牛顿运动定律，负梯度是移动参数空间中粒子所受的力。动量在物理学中定义为质量乘以速度。在动量学习算法中，我们假设单位质量，则速度向量 $v$ 可以被看做是例子的动量。超参数 $\alpha \in [0,1]$ 决定了前面梯度的贡献衰减的速度。基于动量的梯度下降算法更新规则如下：
$$v \leftarrow mv - \epsilon \nabla_{\theta}(\frac{1}{n} \sum_i^n L(f(x^{(i)};\theta), y^{(i)}))$$
$$\theta \leftarrow \theta + v$$

速度 $v$ 累积了梯度元素 $\nabla_{\theta}(\frac{1}{n} \sum_i^n L(f(x^{(i)};\theta), y^{(i)}))$。相对于 $\epsilon, m$ 越大，之前梯度对现在方向的影响也越大。带动量的SGD算法如算法H4.2所示。

在随机梯度下降算法中，步长只是梯度范数乘以学习率；在带动量的算法中，步长取决于梯度序列的大小和排列。当许多连续的梯度指向相同的方向时，步长最大；而没有指向最终方向的梯度并不会使损失下降停止；如果动量算法总是观测到梯度 $g$，那么它会在方向 $-g$ 上不停加速，直到达到最终速度，其步长大小为：
$$\frac{\epsilon ||g||}{1-m}$$
因此，将动量的超参数视为 $\frac{1}{1-m}$ 是有助于理解的。例如，典型值 $m = 0.9$ 对应着最大速度10倍于梯度下降算法。

在实践中，$m$ 的一般取值为0.5、0.9和0.99。与学习率类似，动量 $m$ 也需要随着时间不断调整。一般初始值是一个较小的值，随后会慢慢增大。但是，随着时间的推移，调整 $m$ 没有收缩 $\epsilon$ 重要。

在带动量的随机梯度下降中，当本次梯度下降方向与上次更新量的方向相同时，上次的更新量能够对本次的搜索起到一个正向加速的作用；当本次梯度下降方向与上次更新量的方向相反时，上次的更新量能够对本次的搜索起到一个减速的作用，既减少震荡，又大方向不变（本次梯度下降方向），从而保证了效率和正确的收敛；即使在梯度为0时，由于动量的存在，也仍然会有一定的 $v$ 剩余，使得损失值在最小值附近摇摆。

2.2.2 带动量的随机梯度下降的Python描述

上述的算法可以用下面的公式进行表示，然后改写为python代码

# 首先给出学习率lr，动量参数m
初始速度v=0, 初始x
while True：
    v = m * v - lr * df/dx
    x += v

def draw_SGDMomentum(): 
    model_name = 'SGDMomentum'
    save_path = './Handout04Optimization'
    if not os.path.exists(save_path):
        os.mkdir(save_path) 
        
    plt.figure(figsize=(18, 12))     # 生成画布
    for i in range(9):
        plt.subplot(3,3,i+1)
        plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-")
        # 算法开始
        lr = 0.002
        m = 1 - pow(0.5,i)
        x = -20
        v = 1.0
        GDM_x, GDM_y = [], []
        for it in range(1000):
            GDM_x.append(x), GDM_y.append(f(x))
            v = m * v - lr * df(x)
            x = x + v

        plt.xlim(-20, 20)
        plt.ylim(-2, 10)
        plt.plot(GDM_x, GDM_y, c="r", linestyle="-")
        plt.scatter(GDM_x[-1],GDM_y[-1],90,marker = "x",color="g")
        plt.title('SGDMomentum, lr={:.3f}, m={:.5f}'.format(lr, m))
    plt.savefig(os.path.join(save_path, model_name + ".png" ))

draw_SGDMomentum()

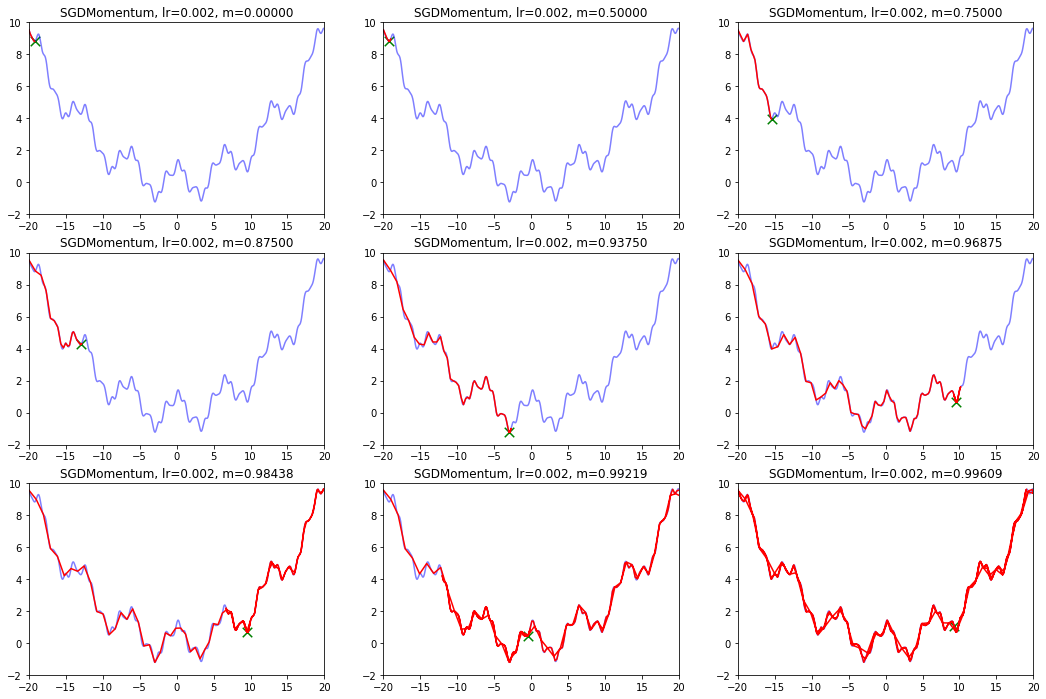
从上图中我们可以看出：

1. lr越小越稳定，太大了很难收敛到最小值上，但是太小的话收敛就太慢了。
2. 动量参数不能太小，0.9以上表现比较好，但是又不能太大，太大了无法停留在最小值处。

2.2.3 随机梯度下降的Paddle描述

# python 1.8
import paddle.fluid.optimizer as optimizer
opt = optimizer.MomentumOptimizer(learning_rate=lr, parameter_list=model.parameters())

# python 2.0
import paddle.optimizer as optimizer
opt = optimizer.Momentum(learning_rate=lr, parameters=model.parameters())

3. 参数初始化策略

---

4. 自适应学习率算法

4.1 AdaGrad算法

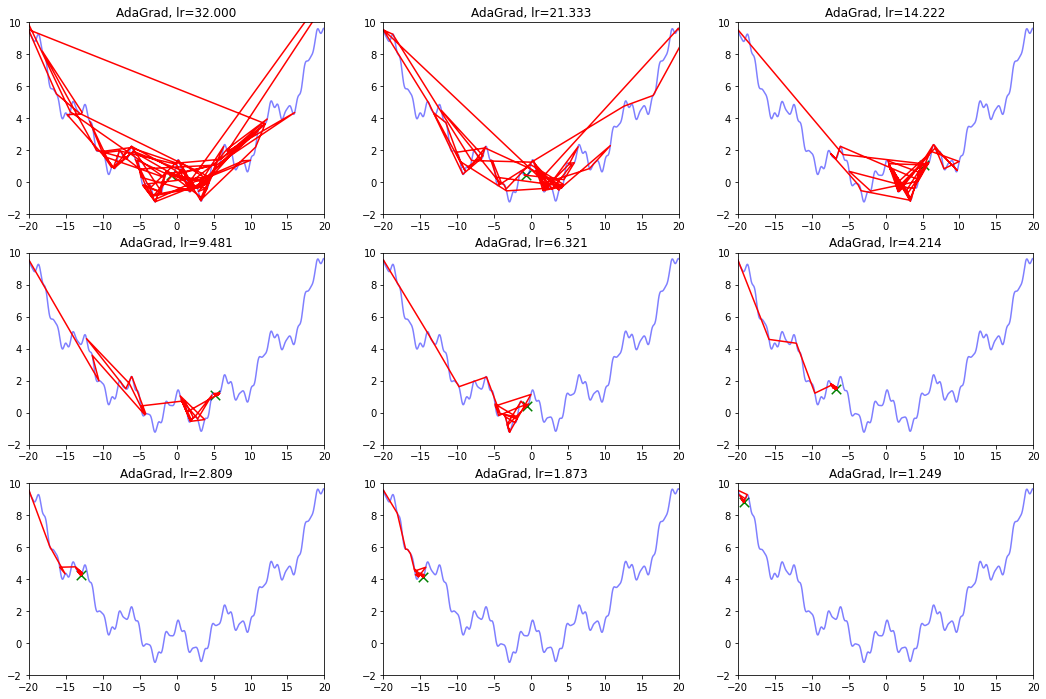
AdaGrad算法的思想是累计历史上出现过的梯度（平方），用积累的梯度平方的总和的平方根，去逐元素地缩小现在的梯度。某种意义上是在自行缩小学习率，学习率的缩小与过去出现过的梯度有关。
缺点是：刚开始参数的梯度一般很大，但是算法在一开始就强力地缩小了梯度的大小，也称学习率的过早过量减少。

• 算法描述：

# 给出学习率lr，delta=1e-7
# 累计梯度r=0，初始x
while True：
      g = df/dx
      r  = r + g*g
      x = x - lr / (delta+ sqrt(r)) * g

def draw_AdaGrad(): 
    model_name = 'AdaGrad'
    save_path = './Handout04Optimization'
    if not os.path.exists(save_path):
        os.mkdir(save_path)     
    
    plt.figure(figsize=(18, 12)) # 生成画布
    for i in range(9):
        plt.subplot(3,3,i+1)
        # 绘制原来的函数
        plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-")
        # 算法开始
        lr = pow(1.5,-i)*32
        delta = 1e-7
        x = -20
        r = 0
        AdaGrad_x, AdaGrad_y = [], []
        for it in range(1000):
            AdaGrad_x.append(x), AdaGrad_y.append(f(x))
            g = df(x)
            r = r + g*g # 积累平方梯度
            x = x - lr /(delta + np.sqrt(r)) * g

        plt.xlim(-20, 20)
        plt.ylim(-2, 10)
        plt.plot(AdaGrad_x, AdaGrad_y, c="r", linestyle="-")
        plt.scatter(AdaGrad_x[-1],AdaGrad_y[-1],90,marker = "x",color="g")
        plt.title('AdaGrad, lr={:.3f}'.format(lr))
    plt.savefig(os.path.join(save_path, model_name + '.png'))

draw_AdaGrad()

4.2 RMSProp算法

AdaGrad算法在前期可能会有很大的梯度，自始至终都保留了下来，这会使得后期的学习率过小。RMSProp在这个基础之上，加入了平方梯度的衰减项，只能记录最近一段时间的梯度，在找到碗状区域时能够快速收敛。

• 算法描述：

# 给出学习率lr，delta=1e-6，衰减速率p
# 累计梯度r=0，初始x
while True：
      g = df/dx
      r  = p*r + （1-p）*g*g
      x = x - lr / (delta+ sqrt(r)) * g

def draw_RMSProp(): 
    model_name = 'RMSProp'
    save_path = './Handout04Optimization'
    if not os.path.exists(save_path):
        os.mkdir(save_path) 
    
    plt.figure(figsize=(18, 18)) # 生成画布

    for i in range(12):
        plt.subplot(4,3,i+1)
        # 绘制原来的函数
        plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-")
        # 算法开始
        lr = pow(1.5,-i)*32
        delta = 1e-6
        rou = 0.8
        x = -20
        r = 0
        RMSProp_x, RMSProp_y = [], []
        for it in range(1000):
            RMSProp_x.append(x), RMSProp_y.append(f(x))
            g = df(x)
            r = rou * r + (1-rou)*g*g # 积累平方梯度
            x = x - lr /(delta + np.sqrt(r)) * g

        plt.xlim(-20, 20)
        plt.ylim(-2, 10)
        plt.plot(RMSProp_x, RMSProp_y, c="r", linestyle="-")
        plt.scatter(RMSProp_x[-1], RMSProp_y[-1], 90, marker = "x", color="g")
        plt.title('RMSProp, lr={:.3f}, rou={:.2f}'.format(lr, rou))
    plt.savefig(os.path.join(save_path, model_name + '.png'))

draw_RMSProp()

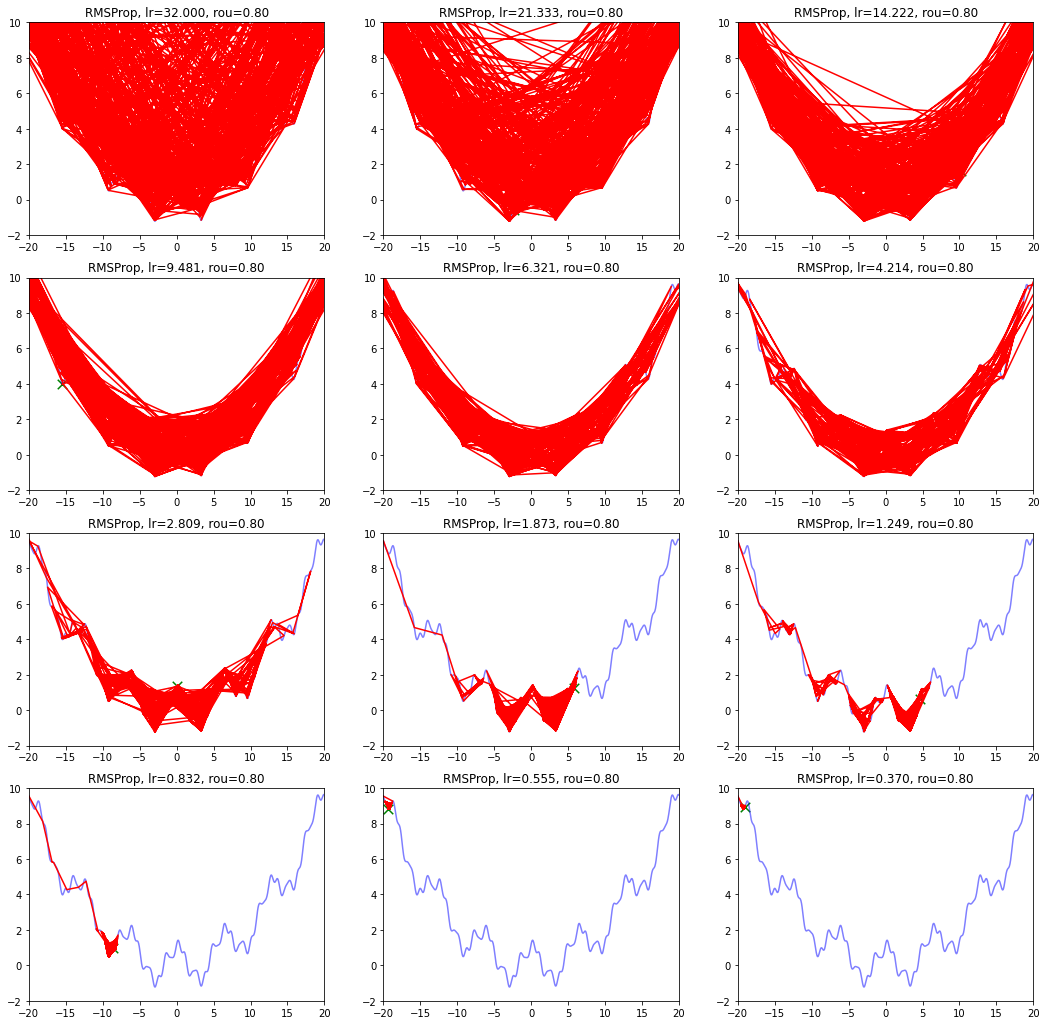
衰减速率情况复杂，建议自行调参.......

4.3 Adam算法

Adam算法和之前类似，也是自适应减少学习率的算法，不同的是它更新了一阶矩和二阶矩，用一阶矩有点像有动量的梯度下降，而用二阶矩来降低学习率。
此外还使用了类似于 $s = \frac{s}{1-p_1^t}$ 这样的公式，这样的公式在t较为小的时候会成倍增加s，从而让梯度更大，参数跑的更快，迅速接近期望点。而后续t比较大的时候，$s = \frac{s}{1-p_1^t}$ 基本等效于s=s，没什么用。

• 算法描述：

# 给出学习率lr，delta=1e-8，衰减速率p1=0.9，p2=0.999 
# 累计梯度r=0，初始x ,一阶矩s=0，二阶矩r=0
# 时间t = 0
while True：
    t += 1
    g = df/dx 
    s = p1*s + (1-p1) *g
    r = p2*r +（1-p2）*g*g

    s = s / (1-p1^t)
    r = r / (1-p2^t)

    x = x - lr / (delta+ sqrt(r)) * s

def draw_Adam(): 
    model_name = 'Adam'
    save_path = './Handout04Optimization'
    if not os.path.exists(save_path):
        os.mkdir(save_path)     
    
    plt.figure(figsize=(18, 48)) # 生成画布
    for i in range(48):
        plt.subplot(12,4,i+1)
        # 绘制原来的函数
        plt.plot(points_x, points_y, c='b', alpha=0.5, linestyle='-')
        # 算法开始
        lr = pow(1.2,-i)*2
        rou1,rou2 = 0.9,0.9  # 原来的算法中rou2=0.999，但是效果很差
        delta = 1e-8
        x = -20
        s,r = 0,0
        t = 0
        Adam_x, Adam_y = [], []
        for it in range(1000):
            Adam_x.append(x), Adam_y.append(f(x))
            t += 1
            g = df(x)
            s = rou1 * s + (1 - rou1)*g
            r = rou2 * r + (1 - rou2)*g*g # 积累平方梯度
            s = s/(1-pow(rou1,t))
            r = r/(1-pow(rou2,t))
            x = x - lr /(delta + np.sqrt(r)) * s

        plt.xlim(-20, 20)
        plt.ylim(-2, 10)
        plt.plot(Adam_x, Adam_y, c='r', linestyle='-')
        plt.scatter(Adam_x[-1], Adam_y[-1], 90, marker='x', color='g')
        plt.title('Adam, lr={:.4f}'.format(lr))
    plt.savefig(os.path.join(save_path, model_name + '.png'))

draw_Adam()

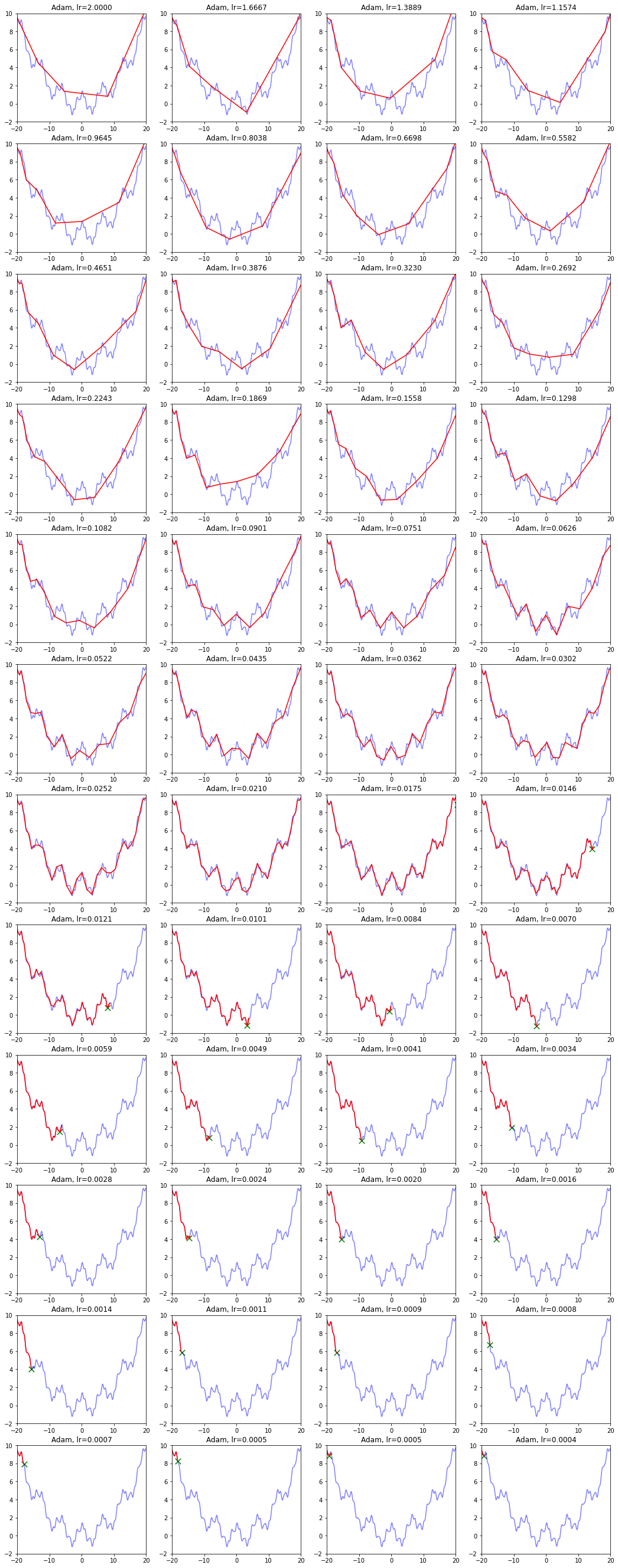
是的，你没有看错，参数不合适的时候，无法收敛。

在算法中仔细研究后才发现，是在t很小的前几步的时候，p2=0.999太大了，导致r = r / (1-p2^t) 中，1-p2^t接近0，r迅速爆炸，百步之内到了inf。后来修改p2=0.9后效果就好得多了。

最后还是Adam效果最好了 ：)，尽管学习率还是需要相当的调参。

5. 学习率衰减策略

学习率策略: 固定fixed, 分段衰减PiecewiseDecay, 余弦退火CosineAnnealingDecay, 指数ExponentialDecay, 多项式PolynomialDecay
MultiStepDecay MultiStep 学习率衰减
MultiStepDecay ultiStep 学习率衰减
https://zhuanlan.zhihu.com/p/22252270
https://zhuanlan.zhihu.com/p/52608023
https://zhuanlan.zhihu.com/p/93624972

5.1 固定学习率

5.2 分段衰减学习率

5.3 指数衰减学习率

5.4 等间隔衰减学习率

5.5 多步长间隔衰减学习率

5.6 多项式衰减学习率

5.7 余弦退火衰减学习率

6. Paddle中的训练优化

6.1 基于 Paddle 2.0 的优化策略

import sys
import os
import paddle
import paddle.optimizer as optimizer

train_parameters = {
    'num_train': 1000,                                        # 训练样本总数
    'total_epoch': 20,                                        # 总迭代次数, 代码调试好后考虑
    'batch_size': 128,                                        # 设置每个批次的数据大小，同时对训练提供器和测试
}

learning_strategy = {                                         # 学习率和优化器相关参数
    'optimizer_strategy': 'Momentum',                         # 优化器：SGD, Momentum, Adagrad, RMSProp, Adam
    'learning_rate_strategy': 'CosineAnnealingDecay',         # 学习率策略: fixed, 分段衰减PiecewiseDecay, 余弦退火CosineAnnealingDecay, 指数ExponentialDecay, 多项式PolynomialDecay
    'learning_rate': 0.01,                                    # 固定学习率
    'momentum': 0.9,                                          # 动量
    'PiecewiseDecay_boundaries': [8, 12, 15],                 # 分段衰减_变换边界(int): 每当运行到epoch时调整一次
    'PiecewiseDecay_values': [0.01, 0.001, 0.0001, 0.00001],  # 分段衰减_步进学习率(float): 每次调节的具体值
    'MultiStepDecay_milestones': [8, 12, 15],                 # 多步长间隔衰减_轮数(int): 按照序列所设置的epoch数进行学习率衰减，衰减率为gamma
    'MultiStepDecay_gamma': 0.1,                              # 多步长间隔衰减_衰减率(float): new_lr = old_lr * gamma
    'StepDecay_step_size': 5,                                 # 等间隔衰减_衰减周期(n:int): 每隔 n个epoch衰减一次
    'StepDecay_gamma': 0.1,                                   # 等间隔衰减_衰减率(float): new_lr = old_lr * gamma
    'ExponentialDecay_gamma': 0.9,                            # 指数衰减_衰减指数(float): new_lr = old_lr * gamma 
    'PolynomialDecay_end_lr': 0.0001,                         # 多项式衰减_最终学习率(float): 最小的最终学习率
    'PolynomialDecay_steps': 5,                               # 多项式衰减_衰减周期(n:int): 经过 n个epoch衰减至最小的最终学习率
    'verbose': False                                           # 日志(bool, [True|False])：是否打印日志
}

args = train_parameters
argsLS = learning_strategy

def learning_rate_setting(verbose=argsLS['verbose'], num_train=args['num_train'], batch_size=args['batch_size'], total_epoch=args['total_epoch']):
    if argsLS['learning_rate_strategy'] == 'PiecewiseDecay':
        lr = optimizer.lr.PiecewiseDecay(boundaries=argsLS['PiecewiseDecay_boundaries'], values=argsLS['PiecewiseDecay_values'], verbose=verbose)
    elif argsLS['learning_rate_strategy'] == 'CosineAnnealingDecay':
        step_each_epoch = num_train // (batch_size * 2)
        T_max = step_each_epoch * total_epoch
        lr = optimizer.lr.CosineAnnealingDecay(learning_rate=argsLS['learning_rate'], T_max=T_max, verbose=verbose)
    elif argsLS['learning_rate_strategy'] == 'ExponentialDecay':
        lr = optimizer.lr.ExponentialDecay(learning_rate=argsLS['learning_rate'], gamma=argsLS['ExponentialDecay_gamma'], verbose=verbose)
    elif argsLS['learning_rate_strategy'] == 'PolynomialDecay':
        lr = optimizer.lr.PolynomialDecay(learning_rate=argsLS['learning_rate'], decay_steps=argsLS['PolynomialDecay_steps'], end_lr=argsLS['PolynomialDecay_end_lr'], verbose=verbose)
    elif argsLS['learning_rate_strategy'] == 'StepDecay':
        lr = optimizer.lr.StepDecay(learning_rate=argsLS['learning_rate'], step_size=argsLS['StepDecay_step_size'], gamma=argsLS['StepDecay_gamma'], verbose=verbose)
    elif argsLS['learning_rate_strategy'] == 'MultiStepDecay':
        lr = optimizer.lr.MultiStepDecay(learning_rate=argsLS['learning_rate'], milestones=argsLS['MultiStepDecay_milestones'], gamma=argsLS['MultiStepDecay_gamma'], verbose=verbose)
    else:                                                            # 固定学习率
        lr = argsLS['learning_rate']
    return lr

def optimizer_setting(model, lr=learning_rate_setting(verbose=False)):
    if argsLS['optimizer_strategy'] == 'SGD':
        # loss下降相对较慢，但是最终效果不错，阶梯型的学习率适合比较大规模的训练数据
        opt = optimizer.SGD(learning_rate=lr, parameters=model.parameters())
    elif argsLS['optimizer_strategy'] == 'Momentum':
        # 阶梯型的学习率适合比较大规模的训练数据
        # momentum:0.9 
        opt = optimizer.Momentum(learning_rate=lr, parameters=model.parameters())
    elif argsLS['optimizer_strategy'] == 'Adagrad':
        # 阶梯型的学习率适合比较大规模的训练数据
        # epsilon=1e-06
        opt = optimizer.Adagrad(learning_rate=lr, parameters=model.parameters())
    elif argsLS['optimizer_strategy'] == 'RMSProp':
        # 阶梯型的学习率适合比较大规模的训练数据
        # rho=0.95, epsilon=1e-06
        opt = optimizer.RMSProp(learning_rate=lr, parameters=model.parameters())
    elif argsLS['optimizer_strategy'] == 'Adam':
        # 能够比较快速的降低 loss，但是相对后期乏力
        # beta1=0.9, beta2=0.999, epsilon=1e-08
        opt = optimizer.Adam(learning_rate=lr, parameters=model.parameters())
    else:
        print('学习率设置错误, 请重新设置。')
    return opt


# 学习率输出测试
if __name__ == '__main__':
    print('当前学习率策略为: {}'.format(argsLS['learning_rate_strategy']))
    linear = paddle.nn.Linear(10, 10)
    lr = learning_rate_setting(verbose=True)
    opt = optimizer_setting(linear, lr)
    if argsLS['learning_rate_strategy'] == 'fixed':
        print('learning = {}'.format(argsLS['learning_rate']))
    else:
        for epoch in range(args['total_epoch']):
            x = paddle.uniform([10, 10])
            out = linear(x)
            loss = paddle.mean(out)
            loss.backward()
            opt.step()
            opt.clear_gradients()
            lr.step() 

    当前学习率策略为: CosineAnnealingDecay
    Epoch 0: CosineAnnealingDecay set learning rate to 0.01.
    Epoch 1: CosineAnnealingDecay set learning rate to 0.009993147673772868.
    Epoch 2: CosineAnnealingDecay set learning rate to 0.009972609476841365.
    Epoch 3: CosineAnnealingDecay set learning rate to 0.009938441702975687.
    Epoch 4: CosineAnnealingDecay set learning rate to 0.009890738003669027.
    Epoch 5: CosineAnnealingDecay set learning rate to 0.009829629131445338.
    Epoch 6: CosineAnnealingDecay set learning rate to 0.009755282581475766.
    Epoch 7: CosineAnnealingDecay set learning rate to 0.009667902132486006.
    Epoch 8: CosineAnnealingDecay set learning rate to 0.009567727288213002.
    Epoch 9: CosineAnnealingDecay set learning rate to 0.009455032620941837.
    Epoch 10: CosineAnnealingDecay set learning rate to 0.009330127018922192.
    Epoch 11: CosineAnnealingDecay set learning rate to 0.009193352839727118.
    Epoch 12: CosineAnnealingDecay set learning rate to 0.009045084971874735.
    Epoch 13: CosineAnnealingDecay set learning rate to 0.008885729807284854.
    Epoch 14: CosineAnnealingDecay set learning rate to 0.00871572412738697.
    Epoch 15: CosineAnnealingDecay set learning rate to 0.008535533905932738.
    Epoch 16: CosineAnnealingDecay set learning rate to 0.008345653031794291.
    Epoch 17: CosineAnnealingDecay set learning rate to 0.008146601955249187.
    Epoch 18: CosineAnnealingDecay set learning rate to 0.007938926261462365.
    Epoch 19: CosineAnnealingDecay set learning rate to 0.0077231951750751345.
    Epoch 20: CosineAnnealingDecay set learning rate to 0.007499999999999999.

6.2 基于 Paddle 1.8 的优化策略

import numpy as np
import paddle.fluid as fluid
import paddle.fluid.optimizer as optimizer

train_parameters = {
    'num_train': 1000,                                        # 训练样本总数
    'total_epoch': 20,                                        # 总迭代次数, 代码调试好后考虑
    'batch_size': 128,                                        # 设置每个批次的数据大小，同时对训练提供器和测试
}

learning_strategy = {                                         # 学习率和优化器相关参数
    'optimizer_strategy': 'Momentum',                         # 优化器：SGD, Momentum, Adam
    'learning_rate_strategy': 'PiecewiseDecay',               # 学习率策略: 固定fixed, 分段衰减PiecewiseDecay, 指数ExponentialDecay,等间隔StepDecay, 步长间隔MultiStepDecay
    'learning_rate': 0.01,                                    # 固定学习率
    'momentum': 0.9,                                          # 动量
    'PiecewiseDecay_boundaries': [8, 12, 15],                 # 分段衰减_变换边界(int): 每当运行到epoch时调整一次
    'PiecewiseDecay_values': [0.01, 0.001, 0.0001, 0.00001],  # 分段衰减_步进学习率(float): 每次调节的具体值
    'MultiStepDecay_milestones': [8, 12, 15],                 # 多步长间隔衰减_轮数(int): 按照序列所设置的epoch数进行学习率衰减，衰减率为gamma
    'MultiStepDecay_decay_rate': 0.1,                         # 多步长间隔衰减_衰减率(float): new_lr = old_lr * gamma
    'StepDecay_step_size': 5,                                 # 等间隔衰减_衰减周期(n:int): 每隔 n个epoch衰减一次
    'StepDecay_decay_rate': 0.1,                              # 等间隔衰减_衰减率(float): new_lr = old_lr * gamma
    'ExponentialDecay_decay_rate': 0.9,                       # 指数衰减_衰减指数(float): new_lr = old_lr * gamma 
}

args = train_parameters
argsLS = learning_strategy

def learning_rate_setting(num_train=args['num_train'], batch_size=args['batch_size'], total_epoch=args['total_epoch']):
    if argsLS['learning_rate_strategy'] == 'PiecewiseDecay':
        lr = fluid.dygraph.PiecewiseDecay(boundaries=argsLS['PiecewiseDecay_boundaries'], values=argsLS['PiecewiseDecay_values'], begin=0)      
    elif argsLS['learning_rate_strategy'] == 'ExponentialDecay':
        lr = fluid.dygraph.ExponentialDecay(learning_rate=argsLS['learning_rate'], decay_steps=1000, decay_rate=argsLS['ExponentialDecay_decay_rate'])
    elif argsLS['learning_rate_strategy'] == 'StepDecay':
        lr = fluid.dygraph.StepDecay(learning_rate=argsLS['learning_rate'], step_size=argsLS['StepDecay_step_size'], decay_rate=argsLS['StepDecay_decay_rate'])
    elif argsLS['learning_rate_strategy'] == 'MultiStepDecay':
        lr = fluid.dygraph.MultiStepDecay(learning_rate=argsLS['learning_rate'], milestones=argsLS['MultiStepDecay_milestones'], decay_rate=argsLS['MultiStepDecay_decay_rate'])
    else:                                                            
        lr = argsLS['learning_rate'] 
    return lr

def optimizer_setting(model, lr):
    if argsLS['optimizer_strategy'] == 'SGD':
        opt = optimizer.SGDOptimizer(learning_rate=lr, parameter_list=model.parameters())
    elif argsLS['optimizer_strategy'] == 'Momentum':
        opt = optimizer.MomentumOptimizer(learning_rate=lr, momentum=argsLS['momentum'], parameter_list=model.parameters())
    elif argsLS['optimizer_strategy'] == 'Adam':
        opt = optimizer.Adam(learning_rate=lr, parameter_list=model.parameters())
    else:
        print('学习率设置错误, 请重新设置。')
    return opt        

# 学习率输出测试
if __name__ == '__main__':
    print('当前学习率策略为: {}'.format(argsLS['learning_rate_strategy']))
    with fluid.dygraph.guard():
        model = fluid.dygraph.nn.Linear(10, 10)        
        lr = learning_rate_setting()
        optimizer = optimizer_setting(model, lr)
        if argsLS['learning_rate_strategy'] == 'fixed':
            print('learning = {}'.format(argsLS['learning_rate']))
        else:
            for i in range(args['total_epoch']):
                x = np.random.uniform(-0.1, 0.1, [10, 10]).astype("float32")
                x = fluid.dygraph.to_variable(x)
                out = model(x)
                loss = fluid.layers.reduce_mean(out)
                optimizer.minimize(loss)
                print("Epoch {}: {} set learning rate to {}.".format(i, argsLS['learning_rate_strategy'], optimizer.current_step_lr()))
 

    当前学习率策略为: PiecewiseDecay
    Epoch 0: PiecewiseDecay set learning rate to 0.009999999776482582.
    Epoch 1: PiecewiseDecay set learning rate to 0.009999999776482582.
    Epoch 2: PiecewiseDecay set learning rate to 0.009999999776482582.
    Epoch 3: PiecewiseDecay set learning rate to 0.009999999776482582.
    Epoch 4: PiecewiseDecay set learning rate to 0.009999999776482582.
    Epoch 5: PiecewiseDecay set learning rate to 0.009999999776482582.
    Epoch 6: PiecewiseDecay set learning rate to 0.009999999776482582.
    Epoch 7: PiecewiseDecay set learning rate to 0.009999999776482582.
    Epoch 8: PiecewiseDecay set learning rate to 0.0010000000474974513.
    Epoch 9: PiecewiseDecay set learning rate to 0.0010000000474974513.
    Epoch 10: PiecewiseDecay set learning rate to 0.0010000000474974513.
    Epoch 11: PiecewiseDecay set learning rate to 0.0010000000474974513.
    Epoch 12: PiecewiseDecay set learning rate to 9.999999747378752e-05.
    Epoch 13: PiecewiseDecay set learning rate to 9.999999747378752e-05.
    Epoch 14: PiecewiseDecay set learning rate to 9.999999747378752e-05.
    Epoch 15: PiecewiseDecay set learning rate to 9.999999747378752e-06.
    Epoch 16: PiecewiseDecay set learning rate to 9.999999747378752e-06.
    Epoch 17: PiecewiseDecay set learning rate to 9.999999747378752e-06.
    Epoch 18: PiecewiseDecay set learning rate to 9.999999747378752e-06.
    Epoch 19: PiecewiseDecay set learning rate to 9.999999747378752e-06.

7. 参考文献

[1] Ian Goodfellow, Yoshua Bengio and Aaron Courville.《Deep Learning深度学习》. 人民邮电出版社. pages 169-200.
[2] SEBASTIAN RUDER. An overview of gradient descent optimization algorithms
[3] Bottou, L. (1998). Online algorithms and stochastic pproximations. In D. Saad, editor, Online Learning in Neural Networks. Cambridge University Press, Cambridge, UK.
[4] Polyak, B. T. (1964). Some methods of speeding up the convergence of iteration methods. USSR Computational Mathematics and Mathematical Physics, 4(5), 1-17
[5] Do we need zero Training loss after achieving zero training error?