【项目017】Softmax回归的实现 | 返回首页
作者:欧新宇(Xinyu OU)
当前版本:Release v1.0
开发平台:Paddle 2.5.2
运行环境:Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案所涉及的数据集仅用于教学和交流使用,请勿用作商用。
最后更新:2024年5月4日
正如上一小节中我们对线性回归的从零开始实现一样,我们认为Softmax回归也是神经网络重要的基础之一,对Softmax回归的实现细节的了解也非常重要。在本小节中,我们会基于Paddle深度学习框架来实现,但在实现过程中也会尽量给出Softmax回归实现的全部流水线,包括数据流水线、模型建立、损失函数的定义以及小批量随机梯度下降优化器的创建等。一个新的数据集Fashion-MNIST将在本项目中被引入。
一、数据准备
Fashion-MNIST数据集是一个与MNIST手写数字数据集相似的数据集,作为机器学习长久以来最基础的数据集,MNIST过于简单,很多算法在测试集上都已经能超过 ,而Fashion-MNIST数据集则相对复杂一些。与MNIST数据集相似,Fashion-MNIST数据集也包含10个类别的 图像,每个类都由6000张训练集(train dataset)图像和1000张测试集(test dataset)图像构成。因此,整个数据集共包含60,000个训练样本和10,000个测试样本。其中,测试集样本只用于评估模型的性能,不参与模型的训练。Fashion-MNIST数据集中的图像如下图所示。

1.1 导入依赖及全局参数设置
import numpy as np # 导入NumPy库
import paddle # 导入Paddle框架
from paddle.vision import transforms # 导入图像预处理模块
from paddle.vision.datasets import FashionMNIST # 导入Fashion-MNIST数据集
from paddle.io import DataLoader # 导入数据迭代读取器
from paddle import nn # 导入神经网络模块
import matplotlib.pyplot as plt # 导入图像显示模块
batch_size = 256 # 定义批量大小
total_epochs = 20 # 定义训练周期数
learning_rate = 0.1 # 定义学习率
1.2 数据载入
在Paddle中,有关数据集的相关调用和处理都保存在 paddle.vision 库中。我们可以通过该库中的内置函数 datasets.FashionMNIST() 来下载FashionMNIST数据集并将其载入到内存中。一般来说,对于原始数据集,我们需要对其进行一定预处理,例如归一化、数据增强等,而Paddle框架中已经内置了常用的数据预处理方法,我们只需要调用即可。例如,我们可以使用 transforms.ToTensor() 将图像数据转换为Tensor格式,并使用 transforms.Normalize() 对图像数据进行归一化处理。更多相关的预处理方法,可以参考第 4.3节 和第 4.4节。
# 1. 定义数据预处理规则
transform = transforms.Compose([
transforms.ToTensor()
])
# 2. 载入数据集
fashion_mnist_train = FashionMNIST(mode='train', transform=transform)
fashion_mnist_test = FashionMNIST(mode='test', transform=transform)
# 3. 显示数据集中样本的数量
print('train: {}, test: {}'.format(len(fashion_mnist_train), len(fashion_mnist_test)))
train: 60000, test: 10000
在第一次载入数据集时,代码会自动去官网下载数据集,并解压到本地。例如,对于Fashion-MNIST数据集的训练集样本,会给出如下的下载信息。
Cache file C:\Users\Administrator\.cache\paddle\dataset\fashion-mnist\train-images-idx3-ubyte.gz not found, downloading https://dataset.bj.bcebos.com/fashion_mnist/train-images-idx3-ubyte.gz
Begin to download
item 6451/6451 [============================>.] - ETA: 0s - 2ms/item
Download finished
Cache file C:\Users\Administrator\.cache\paddle\dataset\fashion-mnist\train-labels-idx1-ubyte.gz not found, downloading https://dataset.bj.bcebos.com/fashion_mnist/train-labels-idx1-ubyte.gz
Begin to download
item 8/8 [============================>.] - ETA: 0s - 53ms/item
Download finished
Cache fileC:\Users\Administrator\.cache\paddle\dataset\fashion-mnist\t10k-images-idx3-ubyte.gz not found, downloading https://dataset.bj.bcebos.com/fashion_mnist/t10k-images-idx3-ubyte.gz
Begin to download
item 1080/1080 [============================>.] - ETA: 0s - 12ms/item
Download finished
Cache file C:\Users\Administrator\.cache\paddle\dataset\fashion-mnist\t10k-labels-idx1-ubyte.gz not found, downloading https://dataset.bj.bcebos.com/fashion_mnist/t10k-labels-idx1-ubyte.gz
Begin to download
item 2/2 [=========================>....] - ETA: 0s - 2ms/item
Download finished
1.3 数据可视化分析
Fashion-MNIST数据集包含10个类别,分别是 t-shirt(T恤)、trouser(裤子)、pullover(套衫)、dress(连衣裙)、coat(外套)、sandal(凉鞋)、shirt(衬衫)、sneaker(运动鞋)、bag(包)和ankle boot(短靴)。为了便于理解,我们可以定义一个函数 get_fashion_mnist_labels() 来通过类别ID获取类别的名称。
# @save datasets.get_fashion_mnist_labels
def get_fashion_mnist_labels(labels):
"""返回Fashion-MNIST数据集的文本标签"""
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
return [text_labels[int(i)] for i in labels]
# 4. 显示测试样本
sample_data, sample_label = fashion_mnist_train[0] # 从训练集中读取一个样本
sample_data = sample_data.reshape([28,28]) # 将图像数据转换为28x28的形状
plt.figure(figsize=(1,1))
plt.imshow(sample_data)
print('sample_data label is "{}".'.format(get_fashion_mnist_labels(sample_label)[0]))
sample_data label is "ankle boot".
1.4 数据读取器
与上一小节相似,我们依然使用 paddle.io.DataLoader 来创建数据读取器。在创建数据读取器时,最常用的三个参数是 batch_size、shuffle 和 drop_last。其中,batch_size 参数用于指定每个小批量包含的样本数;shuffle 参数用于指定是否在每次迭代前随机打乱数据集,它可以让我们随机打乱所有样本,从而无偏见地读取小批量;drop_last 参数用于指定是否扔掉最后一个不完整的小批量,但应注意对测试集进行处理的时候,不能对任何样本进行丢弃。
# 5. 创建数据迭代读取器
train_reader = DataLoader(fashion_mnist_train, batch_size=batch_size, shuffle=True, drop_last=True)
test_reader = DataLoader(fashion_mnist_test, batch_size=batch_size, shuffle=True, drop_last=False)
# 6. 测试数据读取器
for batch_id, (image, label) in enumerate(test_reader()):
print('训练集batch_{}的图像形态:{}, 标签形态:{}'.format(batch_id, image.shape, label.shape))
break
训练集batch_0的图像形态:[256, 1, 28, 28], 标签形态:[256, 1]
二、模型的创建和配置
为了实现Softmax回归,我们首先介绍模型的定义。在Paddle中,我们可以使用 paddle.nn.Linear() 函数来创建各种神经网络模型。对于简单的Softmax回归,在本例中我们只需要创建一个输入层到输出层的线性层即可。首先,我们使用 nn.Flatten 将原始的 [28, 28] 的图像样本变形成一个长度为784维的向量。在后面的章节中,我们会详细介绍有关图像空间结构的问题,这里我们只做简单的拉平处理,并且将这个784维的向量看作是一个样本的特征向量。回想一下,在Softmax回归中,我们的输出与类别是一样多的。因此,在本例中我们可以设置网络的输出维度为10,分别表示Fashion-MNIST数据集中10个类别的概率。因此,模型的权重将构成一个 的矩阵,偏置将构成一个 的向量。与线性回归类似,我们可以使用 nn.Linear() 函数来创建这个线性层。nn.Linear() 有四个重要的参数,分别是in_features, out_features, weight_attr, bias_attr。其中in_features和out_features分别表示输入、输出函数的维度,weight_attr和bias_attr用于定义权重和偏置的初始化方法。本例中,我们依然使用线性回归中的正态分布(均值为0,标准差为0.01)来定义权重,常数0来定义偏置。这两个参数通常也可以不进行专门设置,而使用默认值来定义,此时权重使用Xavier初始化定义,偏置使用常数0定义。
# 1. 定义MLP网络
class SoftmaxRegression(nn.Layer):
def __init__(self, num_classes=10):
super().__init__()
self.features = nn.Sequential(
nn.Flatten(), # 将输入的形状从 [N, C, H, W] 转换成 [N, C*H*W]
nn.Linear(in_features=1*28*28, out_features=num_classes,
weight_attr=paddle.ParamAttr(initializer=nn.initializer.Normal(mean=0.0, std=0.01)),
bias_attr=paddle.ParamAttr(initializer=paddle.nn.initializer.Constant(value=0.0)))
)
def forward(self,input): # 定义网络的前向计算
output = self.features(input)
return output
# 2. 网络测试
if __name__ == '__main__':
model = SoftmaxRegression() # 实例化模型
paddle.summary(model, (10,1,28,28)) # 根据数据的维度输出模型的基本结构
sample_data label is "ankle boot".
训练集batch_0的图像形态:[256, 1, 28, 28], 标签形态:[256, 1]
---------------------------------------------------------------------------
Layer (type) Input Shape Output Shape Param #
===========================================================================
Flatten-1 [[10, 1, 28, 28]] [10, 784] 0
Linear-1 [[10, 784]] [10, 10] 7,850
===========================================================================
Total params: 7,850
Trainable params: 7,850
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.03
Forward/backward pass size (MB): 0.06
Params size (MB): 0.03
Estimated Total Size (MB): 0.12
---------------------------------------------------------------------------
在模型建立后,通常需要对模型的设计做简单的测试,以判断各个核心超参数是否合理,输入是否能通过模型的各个层正常、顺畅地完成前线传播。在Paddle工具包中,我们可以使用 paddle.summary() 函数来输出模型的基本结构。该函数可以完整地输出整个神经网络的所有层的详细信息,也可以输出参数的总量以及模型的占用内存空间的大小。这个输出结果对于我们检查模型的设置非常具有参考性。
三、模型训练与评估
在上一小节的 项目006 中,我们介绍了如何使用Paddle框架来完成线性回归的训练与测试。在本小节中,我们将会介绍如何使用Paddle框架来完成Softmax回归的训练与测试,这个过程与线性回归的实现过程非常相似。不过为了更清晰地展示和理解模型训练的过程,在本项目中我们新增加一个验证函数 evaluation_ch5() 用于在训练中对模型进行验证;同时,我们增加一个过程可视化函数 draw_process_ch5() 用于显示训练过程中的训练误差、训练精度、验证误差和验证精度四个重要输出。
3.1 定义过程可视化函数
对训练过程进行可视化,有助于我们更直观地判断模型是否存在过拟合或欠拟合,同时也帮助我们更直观地判断模型训练的进度。过程可视化通常可以包括训练集的损失值(train_losses), 训练集准确率(train_accs),测试集的损失值(val_losses)和验证集的准确率(val_accs)。一般来说,我们可以在训练过程中动态显示这些数据和迭代次数的关系,也可以在训练结束后展示。值得注意的是, 训练过程中可以每个epoch绘制一个数据点,也可以每个batch绘制一个数据点,也可以每隔n个batch或n个epoch绘制一个数据点。从显示的清晰性考虑,在本章的可视化函数中,除了训练集损失我们使用每个批次(batch)绘制一个数据点,其他数据我们使用每个周期(epoch)绘制一个数据点。另外,需要了解的是,包括后面打印的训练过程的所有输出信息和此处输出的可视化曲线,对于训练集来说展示的都是关于当前批次的信息,而对于验证集来说显示的是整个验证集的信息。
在下面的函数中,参数visualization_log是一个字典,用于存储训练过程中的所有输出信息,它是训练过程中进行记录。在可视化图中,左边的纵坐标指示的是损失值loss的信息,右边的纵坐标指示的是精确度accuracy的信息,横坐标指示的是迭代次数,也即累加的批次序号,图中精度的结点采样自每个训练周期结束时的评估数据。
def draw_process_ch5(visualization_log):
"""绘制训练过程中的训练误差、训练精度、验证误差和验证精度四个重要输出"""
train_accs = visualization_log['train_accs'] # 训练集的精确度
train_losses = visualization_log['train_losses'] # 训练集的损失值
epoch_iters = visualization_log['epoch_iters'] # 每个周期的迭代次数
val_accs = visualization_log['val_accs'] # 验证集的精确度
val_losses = visualization_log['val_losses'] # 验证集的损失值
batch_iters = visualization_log['batch_iters'] # 每个批次迭代的次数
# 第一组坐标轴 Loss
_, ax1 = plt.subplots()
ax1.plot(batch_iters, train_losses, color='orange', linestyle='--', label='train loss')
ax1.plot(epoch_iters, val_losses, color='cyan', linestyle='--', label='validation loss')
ax1.set_xlabel('Iters', fontsize=16)
ax1.set_ylabel('loss', fontsize=16)
max_loss = max(max(train_losses), max(val_losses))
ax1.set_ylim(0, max_loss*1.2)
# 第二组坐标轴 accuracy
ax2 = ax1.twinx()
ax2.plot(epoch_iters, train_accs, 'o-', color='red', markersize=3, label='train accuracy')
ax2.plot(epoch_iters, val_accs, 'o-', color='blue', markersize=3, label='validation accuracy')
ax2.set_ylabel('accuracy', fontsize=16)
max_loss = max(max(train_accs), max(val_accs))
ax2.set_ylim(0, max_loss*1.2)
plt.title('Training and Validation Loss over Epochs', fontsize=18)
handles1, labels1 = ax1.get_legend_handles_labels() # 图例1
handles2, labels2 = ax2.get_legend_handles_labels() # 图例2
plt.legend(handles1+handles2, labels1+labels2, loc='best')
plt.grid()
plt.show()
3.2 定义验证函数
一般来说,在准备好数据集和模型后,就可以将数据送入模型中进行模型训练了。然而,如果仅仅只定义训练函数,我们很难判定模型当前的训练状态如何,我们也无法确定什么时候应该终止训练。对于一个简单的数据集和简单的模型来说,我们可以很快完成训练并在训练结束后对训练的结果进行评估。但是对于包含数百万数据以及几十层的模型,等待训练结束再进行评估就不太合理了。因为每次训练可能花费数十个小时,甚至数天的时间,特别是当我们的GPU并行处理设备并不是特别先进,甚至是干脆使用CPU进行训练的时候。因此,我们很有必要在训练过程中,增加对模型进行验证的能力,以判断模型当前的训练状态如何,并决定是否终止训练。
以上在模型训练过程中对模型性能进行判定的过程通常称为模型验证或在线测试。在整个验证过程中,我们会使用一个称之为验证数据集(val_dataset)的数据子集,在本项目的 1.2 小节中我们已经使用和训练集相同的方法定义了这个子集,并创建了这个子集的数据迭代读取器test_reader。需要注意的是,这里我们使用测试数据来作为验证集使用,这种定义是不严谨。在本书的第 4.2 节 数据准备 中我们对数据的划分进行了更严谨的定义和说明,有兴趣的读者可以参考。在后面的大数据的项目中,我们将使用第 4.2 节 中的严格定义对数据集进行划分。
一般来说,模型的验证需要在训练过程中进行,并且我们通常会同时计算整个模型在验证集上的损失值和精度。因此,定义一个验证函数并在训练的每个周期结束时都调用一次该验证函数对整个验证集进行一次评估是有必要的。下面给出本章中使用的验证函数。
accs = []
losses = []
def evaluation_ch5(model, verbos=False):
model.eval()
for batch_id, (image, label) in enumerate(test_reader()):
predicts = model(image) # 使用模型进行预测
loss = paddle.nn.CrossEntropyLoss()(predicts, label) # 计算损失
acc = paddle.metric.accuracy(predicts, label) # 计算精度
if verbos == True:
if batch_id % 100 == 0:
print("batch_id: {}, loss: {}, acc: {}".format(batch_id, loss.numpy(), acc.numpy()))
accs.append(acc.numpy()) # 记录精度
losses.append(loss.numpy()) # 累加损失和精度
return np.mean(accs), np.mean(losses)
val_accuracy, val_loss = evaluation_ch5(model)
print('[validation] val_loss: {:.4f}, val_accuracy: {:.4f}'.format(val_loss, val_accuracy))
[validation] val_loss: 2.3096, val_accuracy: 0.0805
不难看出,由于模型采用随机初始化进行超参数的初始化,在没有进行训练时的模型准确率和盲猜基本一致。由于数据集的类别数为10,所以准确率就是 附近。
3.4 定义模型训练函数
模型训练的核心部分与模型验证大体相同,区别在于使用的是不同的数据子集,训练过程主要包括如下几个部分:
- 定义输入数据的维度。 输入数据的来源包含两种,一种是通过数据集类获取,此时不需要再次显示定义维度;一种是从外部获取数据,此时需要再次显示定义数据维度,Paddle中可以使用InputSpec来实现。图像输入维度 [None, channel, Width, Height],标签输入维度 [batch, 1],其中None用于匹配batch信息。本例直接调用的是dataset类中的Fashion-MNIST数据集,因此不需要再次定义维度。
- 实例化模型,并载入参数。 在训练中除了损失函数和评价函数是必须的,定义优化器算法也是必须的,这些函数一般来说可以通过 model.prepare() 进行定义。不过,本例为了更多展现训练算法的细节,我们依然手动对每一个处理模块进行定义。
- 在线测试(验证)。 在训练过程中,我们可以每隔一定的周期调用一次验证函数 evaluation(),来对验证集进行测试。一般来说,每个epoch都应该进行一次验证。
- 输出训练过程。 可视化训练和验证的loss和accuracy也是训练中常用的模型选择方法。在训练过程中,可以将周期,批次,损失及精度等信息打印到屏幕。另外,在下面的代码中,我们定义了一个字典visualization_log用来保存训练中的各种状态值,便于后续的可视化输出。
- 训练结束。 在训练过程中,我们通常需要观察训练精度和训练损失值的变化情况,当训练损失值不再继续下降时,就可以停止训练了。
在本项目中,我们每隔100个batch输出一次平均训练误差和准确率;每一轮(epoch)训练之后,使用验证集进行一次测试,在每轮测试中,均输出一次平均验证误差和验证集上的准确率。
visualization_log = { # 初始化状态字典
'train_accs': [],
'train_losses': [],
'val_accs': [],
'val_losses': [],
'batch_iters': [],
'epoch_iters': [],
}
def train_ch5(model):
model.train() # 设置模型为训练模式
num_batch = 0 # 初始化全局批次计数器
# 定义SGD优化函数
optimizer = paddle.optimizer.SGD(learning_rate=learning_rate, parameters=model.parameters())
for epoch in range(total_epochs):
for batch_id, (image, label) in enumerate(train_reader()):
num_batch += 1 # 累加批次计数器
predicts = model(image) # 使用模型进行预测
loss = paddle.nn.CrossEntropyLoss()(predicts, label) # 计算损失
acc = paddle.metric.accuracy(predicts, label) # 计算精度
loss.backward() # 反向传播
if batch_id % 100 == 0: # 每隔100个批次输出一次平均训练误差和准确率
print("epoch: {}, batch_id: {}, loss is: {}, acc is: {}".format(epoch, batch_id, loss.numpy(), acc.numpy()))
optimizer.step() # 更新参数
optimizer.clear_grad() # 清空梯度
visualization_log['train_losses'].append(loss.numpy()[0])
visualization_log['batch_iters'].append(num_batch)
val_accuracy, val_loss = evaluation_ch5(model) # 使用验证集进行一次测试
visualization_log['val_accs'].append(val_accuracy)
visualization_log['val_losses'].append(val_loss)
visualization_log['train_accs'].append(acc.numpy()[0])
visualization_log['epoch_iters'].append(num_batch)
print('[validation] Epoch: {}/{}, val_loss: {:.4f}, val_accuracy: {:.4f}'.format(epoch+1, total_epochs, val_loss, val_accuracy))
model = SoftmaxRegression() # 实例化模型
train_ch5(model) # 调用模型训练函数
epoch: 0, batch_id: 0, loss is: [2.3056672], acc is: [0.078125]
epoch: 0, batch_id: 100, loss is: [0.7271651], acc is: [0.7734375]
epoch: 0, batch_id: 200, loss is: [0.66056216], acc is: [0.765625]
[validation] Epoch: 1/20, val_loss: 1.4771, val_accuracy: 0.4311
epoch: 1, batch_id: 0, loss is: [0.55440885], acc is: [0.83203125]
epoch: 1, batch_id: 100, loss is: [0.5608957], acc is: [0.80078125]
epoch: 1, batch_id: 200, loss is: [0.55349547], acc is: [0.83984375]
[validation] Epoch: 2/20, val_loss: 1.1711, val_accuracy: 0.5580
epoch: 2, batch_id: 0, loss is: [0.49030492], acc is: [0.84375]
epoch: 2, batch_id: 100, loss is: [0.47612697], acc is: [0.8359375]
epoch: 2, batch_id: 200, loss is: [0.4852042], acc is: [0.84375]
[validation] Epoch: 3/20, val_loss: 1.0116, val_accuracy: 0.6234
epoch: 3, batch_id: 0, loss is: [0.49672958], acc is: [0.83984375]
epoch: 3, batch_id: 100, loss is: [0.47253293], acc is: [0.84765625]
epoch: 3, batch_id: 200, loss is: [0.48334074], acc is: [0.8515625]
[validation] Epoch: 4/20, val_loss: 0.9135, val_accuracy: 0.6632
epoch: 4, batch_id: 0, loss is: [0.38208908], acc is: [0.875]
epoch: 4, batch_id: 100, loss is: [0.5077302], acc is: [0.81640625]
epoch: 4, batch_id: 200, loss is: [0.47502327], acc is: [0.84375]
[validation] Epoch: 5/20, val_loss: 0.8461, val_accuracy: 0.6894
epoch: 5, batch_id: 0, loss is: [0.46815044], acc is: [0.84375]
epoch: 5, batch_id: 100, loss is: [0.4274918], acc is: [0.84765625]
epoch: 5, batch_id: 200, loss is: [0.4632907], acc is: [0.8515625]
[validation] Epoch: 6/20, val_loss: 0.7964, val_accuracy: 0.7092
epoch: 6, batch_id: 0, loss is: [0.48013887], acc is: [0.828125]
epoch: 6, batch_id: 100, loss is: [0.53357625], acc is: [0.82421875]
epoch: 6, batch_id: 200, loss is: [0.3982277], acc is: [0.8828125]
[validation] Epoch: 7/20, val_loss: 0.7583, val_accuracy: 0.7245
epoch: 7, batch_id: 0, loss is: [0.38712674], acc is: [0.8828125]
epoch: 7, batch_id: 100, loss is: [0.44092232], acc is: [0.8515625]
epoch: 7, batch_id: 200, loss is: [0.40543973], acc is: [0.86328125]
[validation] Epoch: 8/20, val_loss: 0.7275, val_accuracy: 0.7368
epoch: 8, batch_id: 0, loss is: [0.45583346], acc is: [0.83203125]
epoch: 8, batch_id: 100, loss is: [0.40738553], acc is: [0.8671875]
epoch: 8, batch_id: 200, loss is: [0.41658503], acc is: [0.859375]
[validation] Epoch: 9/20, val_loss: 0.7031, val_accuracy: 0.7463
epoch: 9, batch_id: 0, loss is: [0.42671895], acc is: [0.859375]
epoch: 9, batch_id: 100, loss is: [0.40637243], acc is: [0.85546875]
epoch: 9, batch_id: 200, loss is: [0.5717167], acc is: [0.80859375]
[validation] Epoch: 10/20, val_loss: 0.6824, val_accuracy: 0.7543
epoch: 10, batch_id: 0, loss is: [0.41394615], acc is: [0.84375]
epoch: 10, batch_id: 100, loss is: [0.43803298], acc is: [0.8671875]
epoch: 10, batch_id: 200, loss is: [0.453812], acc is: [0.84765625]
[validation] Epoch: 11/20, val_loss: 0.6644, val_accuracy: 0.7613
epoch: 11, batch_id: 0, loss is: [0.44968873], acc is: [0.82421875]
epoch: 11, batch_id: 100, loss is: [0.5459981], acc is: [0.82421875]
epoch: 11, batch_id: 200, loss is: [0.45526534], acc is: [0.86328125]
[validation] Epoch: 12/20, val_loss: 0.6496, val_accuracy: 0.7672
epoch: 12, batch_id: 0, loss is: [0.42017344], acc is: [0.85546875]
epoch: 12, batch_id: 100, loss is: [0.51122314], acc is: [0.83203125]
epoch: 12, batch_id: 200, loss is: [0.4028713], acc is: [0.875]
[validation] Epoch: 13/20, val_loss: 0.6366, val_accuracy: 0.7722
epoch: 13, batch_id: 0, loss is: [0.42107573], acc is: [0.8515625]
epoch: 13, batch_id: 100, loss is: [0.42581317], acc is: [0.87890625]
epoch: 13, batch_id: 200, loss is: [0.4281903], acc is: [0.859375]
[validation] Epoch: 14/20, val_loss: 0.6259, val_accuracy: 0.7764
epoch: 14, batch_id: 0, loss is: [0.42132264], acc is: [0.8671875]
epoch: 14, batch_id: 100, loss is: [0.43990475], acc is: [0.8359375]
epoch: 14, batch_id: 200, loss is: [0.48197567], acc is: [0.8359375]
[validation] Epoch: 15/20, val_loss: 0.6167, val_accuracy: 0.7799
epoch: 15, batch_id: 0, loss is: [0.440462], acc is: [0.86328125]
epoch: 15, batch_id: 100, loss is: [0.39327475], acc is: [0.86328125]
epoch: 15, batch_id: 200, loss is: [0.45190835], acc is: [0.859375]
[validation] Epoch: 16/20, val_loss: 0.6077, val_accuracy: 0.7833
epoch: 16, batch_id: 0, loss is: [0.4445534], acc is: [0.83984375]
epoch: 16, batch_id: 100, loss is: [0.47796422], acc is: [0.83984375]
epoch: 16, batch_id: 200, loss is: [0.42603287], acc is: [0.87109375]
[validation] Epoch: 17/20, val_loss: 0.5995, val_accuracy: 0.7863
epoch: 17, batch_id: 0, loss is: [0.4553969], acc is: [0.8671875]
epoch: 17, batch_id: 100, loss is: [0.39542478], acc is: [0.85546875]
epoch: 17, batch_id: 200, loss is: [0.43753988], acc is: [0.86328125]
[validation] Epoch: 18/20, val_loss: 0.5927, val_accuracy: 0.7888
epoch: 18, batch_id: 0, loss is: [0.41297153], acc is: [0.859375]
epoch: 18, batch_id: 100, loss is: [0.40131187], acc is: [0.83984375]
epoch: 18, batch_id: 200, loss is: [0.4251083], acc is: [0.8515625]
[validation] Epoch: 19/20, val_loss: 0.5861, val_accuracy: 0.7913
epoch: 19, batch_id: 0, loss is: [0.3919644], acc is: [0.84765625]
epoch: 19, batch_id: 100, loss is: [0.33163086], acc is: [0.88671875]
epoch: 19, batch_id: 200, loss is: [0.3932777], acc is: [0.859375]
[validation] Epoch: 20/20, val_loss: 0.5798, val_accuracy: 0.7938
下面我们调用训练过程可视化函数将训练过程中记录的损失值和精度值绘制出来。
draw_process_ch5(visualization_log)
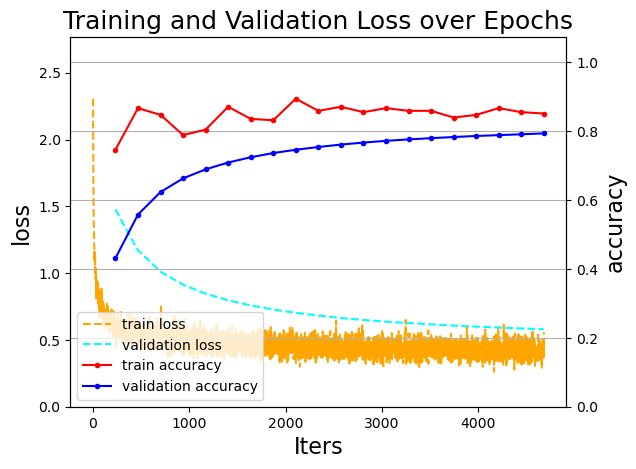
从上图中,我们可以观察到,在经过了10个周期的训练后,训练损失和验证损失都在持续下降,并在最后阶段基本保持稳定。相似地,训练精度和验证精度也在持续上升。此外,我们并没有观察到明显的过拟合问题。说明整个训练过程中的各个超参数配置是基本合理的,当然细微的调整应该可以获得更好的结果。
四、模型的推理与预测
在完成了模型的训练后,我们就可以使用训练好的模型对新的数据进行预测。在Paddle中,模型的预测过程与模型的验证评估过程非常相似,也可以通过定义一个函数来完成。在下面的代码中,我们定义了一个预测函数,该函数接收一个模型和一个图片样本作为输入,并使用该模型对输入数据进行预测。
import random
# 1. 定义一个预测函数
def predict_ch5(model, data):
model.eval() # 设置模型为评估模式
predicts = model(data) # 使用模型进行预测
predict_result = paddle.argmax(predicts, axis=1) # 获取预测结果(概率最大的一个类别)
return predict_result
# 2. 从测试数据集中随机获取一个样本
id = random.randint(0, len(fashion_mnist_test)) # 随机获取一个样本的索引值
test_data, test_label = fashion_mnist_test[id] # 获取测试数据集和标签
# 3. 调用预测函数给定样本进行评估预测
res = predict_ch5(model, test_data) # 使用模型进行预测
plt.figure(figsize=(1,1)) # 设置图片大小
plt.imshow(test_data.reshape([28,28])) # 绘制图片
print('GrandTruth: {}, Prediction: {}'.format(get_fashion_mnist_labels(test_label), get_fashion_mnist_labels(res)))
GrandTruth: ['dress'], Prediction: ['dress']