【项目007】基于多层感知机的手势识别（学生版）显示答案 | 返回首页

作者：欧新宇（Xinyu OU）
当前版本：Release v2.0
开发平台：Paddle 2.5.2
运行环境：Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案所涉及的数据集仅用于教学和交流使用，请勿用作商用。

最后更新：2024年5月9日

【实验说明】

一、实验目的

熟悉神经网络的基本结构，包括层（输入、输出、隐层）、损失函数、激活函数、优化方法等
学会使用mini-batch方法实现深度神经网络的训练并进行预测
学会保存模型，并使用保存的模型进行预测（即应用模型到生产环境）
学会使用PaddlePaddle构建多层感知机

二、实验要求

重点掌握多层感知机的基本结构，并学会使用PaddlePaddle进行模型构建
熟练掌握基于mini-batch的训练方法的Python实现
掌握模型的保存和读取方法，能根据需求的不同选择合适的保存模式
学会在训练过程中加入验证代码实现 训练+验证 配合

三、思维导图

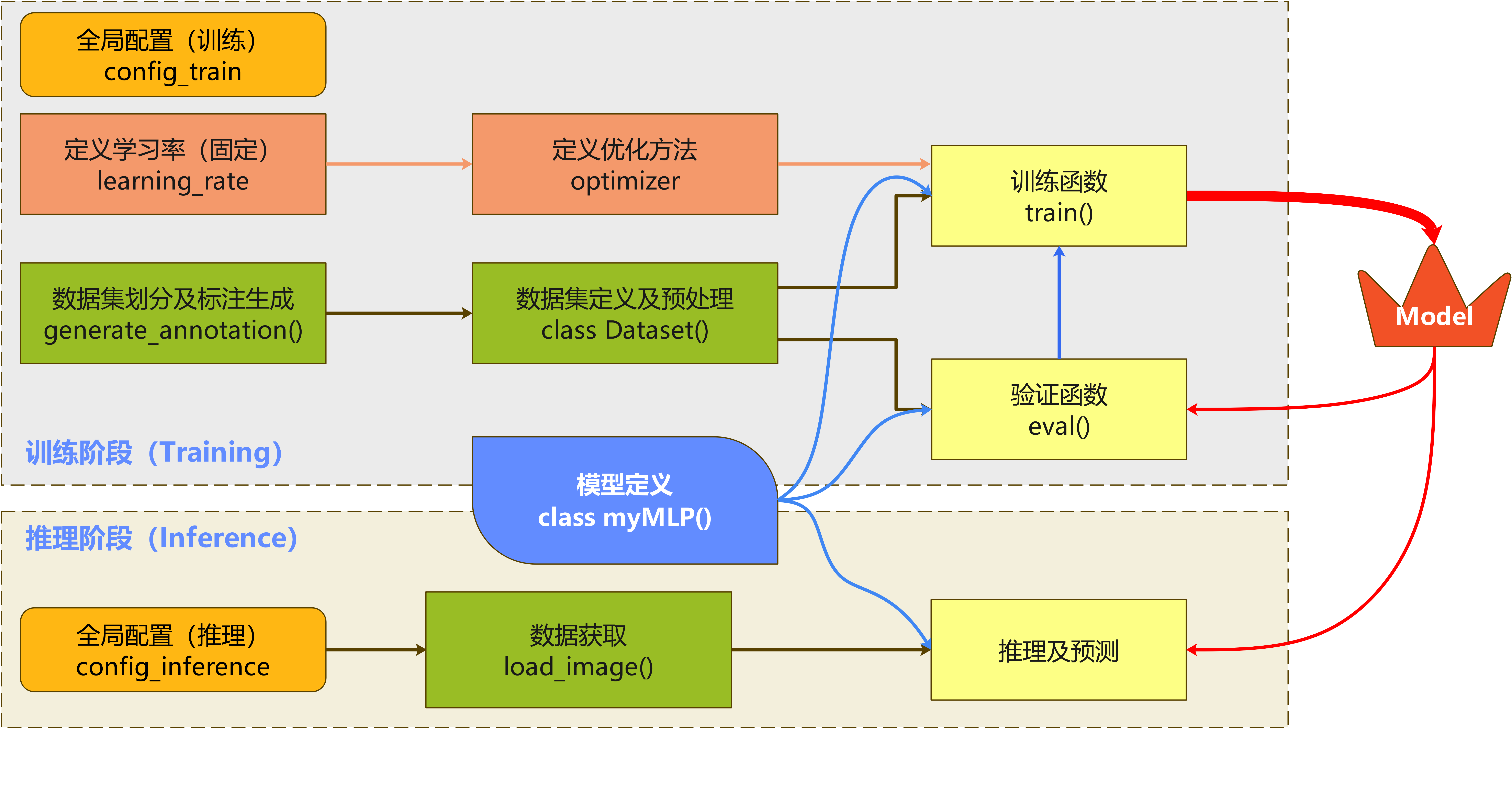
四、目录结构

本项目目录结构说明（可根据实际情况进行修改）
- 数据集根目录：D:\WorkSpace\ExpDatasets\Gestures
- 模型保存目录：D:\WorkSpace\ExpResults\Project007FFNGestures
- 最终模型名称：final_model

【实验一】数据准备

实验难度：中等
实验摘要：利用Paddle内置库paddle.io实现数据集的定义和数据读取器的创建，并且能够对数据集类和数据读取器进行简单的测试。
实验目标：
1. 理解训练集、验证集、测试集在模型训练中的作用
2. 初步学会通过实例化数据集类来定义数据集及创建数据迭代读取器
3. 初步理解图像的基本预处理方法，包括尺度变换，像素值归一化，数据形态变换
4. 理解如何利用transforms函数实现数据的预处理，包括将数据转换为Paddle要求的Tensor模式
实验建议：
1. 本项目不要求对数据集实现标注生成、拆分、清洗等操作，可直接下载项目提供的数据集，并直接载入数据集中提供的数据标注生成工具。
2. 本项目不要求对数据进行数据增广操作，但建议按照标准数据类定义框架对数据集进行解析

1.1 导入依赖及全局参数设置

# 0. 导入依赖库
import os
import cv2
import numpy as np
import paddle
paddle.vision.set_image_backend('cv2')

# 1. 定义数据集列表文件路径
dataset_name      = 'Gestures'
project_name      = 'Project007FFNGestures'
dataset_path      = 'D:\\Workspace\\ExpDatasets\\'
dataset_root_path = os.path.join(dataset_path, dataset_name)

train_list = os.path.join(dataset_root_path, 'train.txt')
val_list = os.path.join(dataset_root_path, 'val.txt')
test_list = os.path.join(dataset_root_path, 'test.txt')

# 2. 定义训练参数
input_size        = [100, 100, 3]  
total_epoch       = 30               # 迭代次数, 代码调试好后考虑Epochs_num = 500-600
eval_interval     = 1                # 设置在训练过程中,每隔一定的周期进行一次测试
log_interval      = 10               # 训练日志显示间隔
learning_rate     = 0.001            # 学习率 

# 3. 定义输出参数
np.set_printoptions(precision=5, suppress=True) # 设置numpy的精度，用于打印输出

architecture      = 'MLP'
result_root_path  = 'D:\\Workspace\\ExpResults\\'
final_models_path = os.path.join(result_root_path, project_name, 'final_model')

1.2 数据集介绍

手势识别 数据集是由土耳其一所中学制作，数据集由 Data文件夹 中的训练验证数据和 Infer文件夹 中的预测数据组成，包含0-9共10种数字的手势。以下为该数据集的官方描述：

This dataset is prepared by Turkey Ankara Ayrancı Anadolu high school students.
Image size: 100 x 100 pixels
Color space: RGB
Number of classes: 10 (Digits: 0-9)
Number of participant students: 218
Number of samples per student: 10
Dataset Url：https://github.com/ardamavi/Sign-Language-Digits-Dataset

Project00701GestureExamples

数据集下载：https://aistudio.baidu.com/aistudio/datasetdetail/54000

1.3 生成数据列表

根据原始数据集的图片，生成列表文件。此处，按照7:1:2的比例进行训练集、验证集、测试集的划分，并将划分好的数据分别保存成四个列表文件：train.txt, val.txt, trainval.txt, test.txt文件中, 同时生成数据集的基本信息文件dataset_info.json. 数据列表文件的基本格式如下：

D:\Workspace\ExpDatasets\Gestures\Data\0\IMG_5991.JPG 0
D:\Workspace\ExpDatasets\Gestures\Data\1\IMG_1129.JPG 1
D:\Workspace\ExpDatasets\Gestures\Data\1\IMG_1139.JPG 1

其中，第一项为图片的保存路径，第二项为该图片的分类标签。中间使用一个Tab（或者1个空格）进行分隔。值得注意的是，数据（图片）保存的路径可以使用绝对路径也可以使用相对路径，但为了避免不必要的麻烦和错误，建议使用绝对路径进行索引。

为简化代码，在本例中请直接下载 Gestures数据集，并调用数据集中写好的数据集划分代码 generate_annotation.py。下面为调用数据集划分的代码，该代码只需要执行一次。

!python "D:\\Workspace\\ExpDatasets\\Gestures\\generate_annotation.py"

图像列表已生成, 其中训练验证集样本1642，训练集样本1432个, 验证集样本210个, 测试集样本420个, 共计2062个。

1.4 定义数据集

深度学习的数据在送入模型之前，通常需要进行一系列的处理，包括转换数据格式、数据集划分、数据形状变形、制作数据迭代读取器、数据增广等。因此，通过封装技术实现对这些操作的整合有利于模型设计的规范和简洁。在Paddle中，有两个核心步骤实现数据集的定义和加载：

定义数据集：在paddle框架中提供了paddle.io.Dataset库实现数据集的定义，它可以将磁盘中保存的原始图片、文字等样本和对应的标签映射到Dataset，并将路径和图像标注分别转换为图像矩阵和标签矩阵，方便后续通过索引（index）读取数据。在 Dataset 中还可以对图像进行预处理操作，包括基本处理和图像增广，其中基本处理包括图像尺度变换、通道变换、数据类型变换、数据标准化和数据归一化；图像增广包括图像的旋转、仿射变换、色彩变换、增加噪声图像等。
迭代读取数据集：在paddle框架中可使用 paddle.io.DataLoader 来实现数据集的迭代读取。它能够自动将数据集的样本进行分批（batch）、乱序（shuffle）等操作，方便训练时迭代读取，同时还支持多进程异步读取功能可加快数据读取速度。在DataLoader的参数中，batch_size 表示每次进行训练的数据批次的图片数量；shuffle 表示是否对当前读入的数据进行打乱，一般来说对于训练集是需要进行打乱的，而对于验证和测试集，由于每次都是对所有样本进行一次轮询，所以不需要进行打乱；drop_last 表示在分批次之后，最后剩余的样本是否进行丢弃，同样由于测试和验证需要对所有样本进行轮询，因此通常设置为False，而对于训练数据，如果训练数据足够多，通常可以设置为True，如果训练数据比较少，那么建议设置成Fasle，以尽量保证样本的多样性。

import paddle.vision.transforms as T
from paddle.io import DataLoader

# 1. 定义数据集
class Dataset(paddle.io.Dataset): 
    # 步骤一：继承 paddle.io.Dataset 类
    def __init__(self, dataset_root_path, mode='test'):
        # 步骤二：实现 __init__ 函数，初始化数据集，将样本和标签映射到列表中
        assert mode in ['train', 'val', 'test', 'trainval']
        self.data = []                              # 创建空列表文件，用于保存数据的路径和标签
        
        # 读取数据集列表文件，并将路径路径和标签进行拆分，其中测试集若不存在标签则复制为"-1"
        with open(os.path.join(dataset_root_path, mode+'.txt')) as f:
            for line in f.readlines():
                info = line.strip().split('\t')  # 以制表符为分割依据
                image_path = os.path.join(dataset_root_path, info[0].strip())   # 数据的真实路径，根据实际情况进行修改
                
                if len(info) == 2: # 包含标签的数据
                    self.data.append([image_path, info[1].strip()])
                elif len(info) == 1: # 不包含标签的数据
                    self.data.append([image_path, -1])

        # 传入定义好的数据处理方法，作为自定义数据集类的一个属性
        self.transforms = T.ToTensor()
    
    # 根据索引获取单个样本
    def __getitem__(self, index):
        # 步骤三：实现 __getitem__ 函数，定义指定 index 时如何获取数据，并返回单条数据（样本数据、对应的标签） 
        # Q1：定义属于读取及预处理方法，实现以下八个步骤
        # 1. 根据索引，从列表中取出一个图像，并将数据拆分成路径和列表
        image_path, label = self.data[index]
        # 2. 使用cv2进行数据读取可以强制将的图像转化为彩色模式，其中0为灰度模式，1为彩色模式
        img = cv2.imread(image_path, 1)
        # 3. 将图像尺度resize为指定尺寸
        img = cv2.resize(img, (100, 100))
        # 4. 将图像数据类型转化为float32（Paddle默认的内部数据格式）
        img = np.array(img).astype('float32')
        # 5. 将像素值归一化到[0, 1]之间，仅在MLP中使用
        img = img/255
        # 6. 调整数据形状paddle默认张量格式
        img = self.transforms(img)
        # 7. 将图像拉成一维向量
        img = paddle.reshape(img, [3*100*100])
        # 8. CrossEntropyLoss要求label格式为int，将Label格式转换为 int
        label = np.array(label, dtype='int64')
        
        return img, label
                
    # 获取样本总数    
    def __len__(self):    
        # 步骤四：实现 __len__ 函数，返回数据集的样本总数    
        return len(self.data)

########################################################################################
# Q2. 实例化数据类
dataset_train = 
dataset_val = 
dataset_test = 

# Q3. 创建迭代读取器
train_reader = 
val_reader = 
test_reader = 

# 4. 测试读取器
if __name__ == "__main__":    
    print('数据集包含训练数据{}个，验证数据{}个，测试数据{}个，训练验证数据{}个。'.format(len(dataset_train),len(dataset_val),len(dataset_test),len(dataset_trainval)))
    print('数据的形态为：{}'.format(dataset_val[0][0].shape)) 

    for i, (image, label) in enumerate(val_reader()):
        print('验证集batch_{}的图像形态:{}, 标签形态:{}'.format(i, image.shape, label.shape))
        break

数据集包含训练数据1432个，验证数据210个，测试数据420个。
数据的形态为：[30000]
验证集batch_0的图像形态:[64, 30000], 标签形态:[64]

【实验二】模型配置和训练

实验难度：困难
实验摘要：设计一个多层感知机模型，并利用该模型在训练集上进行训练，在验证集和测试集上进行评估。
实验目标：
1. 理解训练集、验证集及测试集在模型训练中的作用；
2. 掌握前馈神经网络的构建方法，并能够根据体系结构图实现模型的训练设计；
3. 学会设计两层循环完成模型的训练；
4. 理解并学会使用在线测试和离线测试两种方法。
实验建议：
1. 重点关注训练、验证和测试集的使用场合，通常不能进行错误使用；
2. 对于MLP模型，输入样本应该规范成一维向量进行输入；
3. 重点理解训练过程中两层循环的作用，其中外层循环用于实现多个epoch的迭代，内层循环用于实现单个epoch内不同batch的迭代。

2.1 配置网络

Paddle的组网可以使用paddle.nn.Layer组网方式，这也是在Paddle2.0之后比较推荐的方法，它主要包括三个步骤：
构建一些比较复杂的网络结构时，可以选择该方式，组网包括三个步骤：

创建一个继承自 paddle.nn.Layer 的类；
在类的构造函数 __init__ 中定义组网用到的神经网络层（layer）；
在类的前向计算函数 forward 中使用定义好的 layer 执行前向计算。

在本范例中，我们使用一个5层的前馈神经网络（多层感知机）对手势识别数据集进行建模。其中第一层为输入层，后面紧跟一个大小为100的隐层和两个大小为256的隐层，以及一个大小为10的输出层。其中，输出层的每个神经元对应于MNIST的类别数，即0-9的10个数字。最后使用交叉熵函数求损失，并用Softmax分类器输出类别。

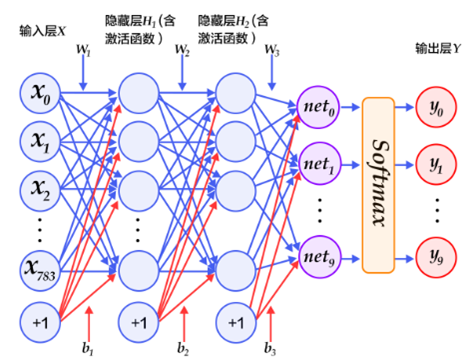
Project00702Architecture

输入层 $X$ ：手势识别数据集中的每个样本都为分辨率为 3×100×100 像素的彩色图片，根据前馈神经网络的结构。我们将其拉伸成一个向量3×100×100的向量进行输入，其维度为[N,3×100×100]。第一个维度是批大小，即batch_size为N的向量；第二个维度是将整幅彩色图像展开成向量形式，向量长度为3×100×100。
隐藏层 $H_1$ ：输入是输入层，即长度为3×100×100的向量，输出是长度为100的向量，激活函数为ReLU。
隐藏层 $H_2$ ：输入为上一层的输出，即长度为100的向量，输出是长度为256的向量，激活函数为ReLU。
隐藏层 $H_3$ ：输入为上一层的输出，即长度为256的向量，输出是长度为256的向量，激活函数为ReLU。
输出层 $Y$ ：输入为上一层的输出，即长度为256的向量，输出是长度为10的向量，即10个节点的Softmax分类器层，对应于手势识别数据集的10个类别。所有的输出节点组成一个N=10维的向量，经过Softmax分类器后，将归一化为N个 [0,1] 的实数，其值为该样本属于这N个类别的概率，并且有 $\sum_{n=0}^9 y_n = 1$ ，即所有类别概率的和为1。对应的标签Label为正确类的One-hot向量。

使用动态图模式比静态图要简单很多，只需要定义模型结构即可。模型定义需要使用Object-Oriented-Designed面向对象的类进行定义。以下为该多层感知机的网络构建函数。此处我们使用动态图模式进行网络结构的定义。首先定义了一个多层感知机的类class myMLP(paddle.nn.Layer)。在该类别使用__init__(self)对参数进行初始化，并定义前向传播forward(self)方法。在MLP中，我们主要用到两个类，分别是nn.Linear()和nn.ReLU()。其中，nn.Linear()是线性核，可以理解为一个全连接层，它主要包括两个参数，分别是输入特征的维度in_features和输出特征的维度out_features，nn.ReLU()没有需要配置的参数，它实现将特征进行ReLU非线性变换。

from xml.etree.ElementTree import QName
import paddle.nn as nn

# 1. 定义MLP网络
class myMLP(nn.Layer):
    def __init__(self, num_classes=10):
        super(myMLP,self).__init__()
        self.num_classes = num_classes
        self.features = nn.Sequential(
            # Q4：根据体系结构图和说明文档设计模型结构
            

            
        )

    def forward(self, input):
        output = self.features(input)
        
        return output

# 2. 网络测试
if __name__ == '__main__':
    model = myMLP()                          # 实例化模型
    paddle.summary(model, (10,100*100*3))    # 根据数据的维度输出模型的基本结构

    ---------------------------------------------------------------------------
     Layer (type)       Input Shape          Output Shape         Param #    
    ===========================================================================
       Linear-1        [[10, 30000]]          [10, 100]          3,000,100   
        ReLU-1          [[10, 100]]           [10, 100]              0       
       Linear-2         [[10, 100]]           [10, 256]           25,856     
        ReLU-2          [[10, 256]]           [10, 256]              0       
       Linear-3         [[10, 256]]           [10, 256]           65,792     
        ReLU-3          [[10, 256]]           [10, 256]              0       
       Linear-4         [[10, 256]]            [10, 10]            2,570     
    ===========================================================================
    Total params: 3,094,318
    Trainable params: 3,094,318
    Non-trainable params: 0
    ---------------------------------------------------------------------------
    Input size (MB): 1.14
    Forward/backward pass size (MB): 0.09
    Params size (MB): 11.80
    Estimated Total Size (MB): 13.04
    ---------------------------------------------------------------------------

2.2 模型训练及评估

在准备好数据集和模型后，就可以将数据送入模型中启动训练评估了，概括地讲包括如下几步：

模型训练：训练包括多轮迭代（epoch），每轮迭代遍历一次训练数据集，并且每次从中获取一小批（mini-batch）样本，送入模型执行前向计算得到预测值，并计算预测值（predict_label）与真实值（true_label）之间的损失函数值（loss）。执行梯度反向传播，并根据设置的优化算法（optimizer）更新模型的参数。观察每轮迭代的 loss 值减小趋势，可判断模型训练效果。该步骤使用训练集/训练验证集。
模型评估：将验证数据集送入训练好的模型进行评估，得到预测值，计算预测值与真实值之间的损失函数值（loss），并计算评价指标值（metric），便于评估模型效果。该步骤使用验证集。
模型推理：将待测试的数据（样本）送入训练好的模型执行推理，观察并验证推理结果（标签）是否符合预期。该步骤使用测试集或自定义数据。

2.2.1 定义验证函数

模型测试一般包含两个类型，分别是：

在线测试，在线测试通常是针对验证集进行，并在训练过程中，每隔一定的周期输出一次精度和损失值
离线测试，指在模型训练结束之后，使用测试集进行的评估。

两种测试模式，在代码上基本上是一致的，只是所使用的数据不同。因此，我们可以定义一个eval()函数来实现代码复用，在进行评估时，分别调用val_reader()和test_reader()的即可。

测试部分的具体流程包括：

定义结果容器保存运行结果，包括top1精度，top5精度，损失losses
由于验证/测试只需要对数据进行一轮推理，因此我们只需要基于批次batch的进行一层循环测试即可。此处，我们可以直接调用paddle的eval_batch()函数实现推理。该函数会根据model.prepare()所定义的损失函数和衡量标准进行自动计算。通常，在分类任务中，我们会使用交叉熵来计算损失，并使用精度来对结果进行衡量。
将eval_batch()获得的结果进行输出

# 模型测试函数，可同时用于在线测试和离线测试
def eval(model, data_reader, verbose=0):
    accuracies_top1 = []
    accuracies_top5 = []
    losses = []
    n_total = 0
    
    # Q5： 设计单层循环，实现模型的测试，可以根据输入的数据集，分别对测试集和验证集进行测试
    for batch_id, (image, label) in enumerate(data_reader):





    return avg_loss, avg_acc_top1, avg_acc_top5

2.2.2 定义训练函数

在做好模型训练的前期准备工作后，就可以进行训练了。模型的训练过程通常采用二层循环嵌套方式：内层循环完成整个数据集的一次遍历，采用分批次方式；外层循环根据设置的训练轮次完成数据集的多次遍历。因此需要指定三个关键参数，分别是定义好的模型（Model）、模型迭代读取器（DataLoader）和训练轮次（Epoch）。其中定义好的模型包含了模型的基本结构和前向传输的规则，模型迭代读取器包含了数据样本和内训中每个批次的训练样本数，训练轮次指定了训练时遍历数据集的次数，即外循环轮次。

与验证/测试类似，为了简便，我们可以使用Paddle内置的训练函数model.train_batch()来实现训练。在使用该函数训练之前，我们还需要对模型model进行一些配置，包括实例化实例化模型，配置模型的输入参数，定义优化器，定义评价函数等。具体包括：

    # 设置输入样本的维度
    input_spec = InputSpec(shape=[None, 3*100*100], dtype='float32', name='image')
    label_spec = InputSpec(shape=[None, 1], dtype='int64', name='label')

    # 设置学习率、优化器、损失函数和评价指标
    lr = learning_rate
    optimizer = optimizer.Adam(learning_rate=lr, parameters=model.parameters()) 
    model.prepare(optimizer,
                  paddle.nn.CrossEntropyLoss(),
                  paddle.metric.Accuracy(topk=(1,5)))

此外，我们还可以定义一些提示性的信息用于观察训练过程，例如如下形式：

Epoch:1/30, batch:20, train_loss:[2.47361], acc_top1:[0.09375], acc_top5:[0.56250](0.43s)    
[validation] Epoch:1/30, val_loss:[0.04288], val_top1:[0.10000], val_top5:[0.50000]
最优top1测试精度:0.10000 (epoch=1)

以上信息包括周期信息，批次信息，训练和验证损失，top1精度，top5精度以及程序运行时间等。

在Paddle中，模型的保存和载入有很多种模式，但是最常用的是还是基于model.save()来实现，具体有两种情况：

model.save(path)：默认情况training=True，当training设置为True时，保存的模型容量比较大，此时包括模型的结构、所有参数以及模型训练过程中的状态。我们可以通过载入此时的模型进行模型的验证与评估，也可以载入此时的模型实现模型的恢复训练和迁移训练。此时的模型，我们一般称之为调优模型。
model.save(path, training=False)：当training设置为False时，模型只保留用于推理的参数，换句话说此时的模型无法载入进来用于评估其准确性，仅仅只能通过前向推理获得输出。因此此时的模型我们一般称之为部署模型。

关于两种模型的载入方法，请参考后面的示例代码。

值得注意的是

在每一轮的训练中，每N个batch之后会输出一次平均训练误差和准确率。每一轮训练之后，使用测试集进行一次测试，在每轮测试中，均打输出一次平均测试误差和准确.
在训练过程中，我们可以每个（若干个）epoch都执行一次模型保存，这种方式一般应用在复杂的模型和大型数据集上。这种经常性的模型保存，有利于我们执行EarlyStopping策略，当我们发现运行曲线不再继续收敛时，就可以结束训练，并选择之前保存的最好的一个模型作为最终的模型。
在本项目的代码中，我们设置了一个最优精度，并将每次对验证集的评估与最优精度进行对比，若当前的验证精度比最优精度更好，则将当前轮次的模型保存为最终模型；若当前验证精度比最优精度差，则跳过，继续进行训练。

import os
import time
import json
import paddle
from paddle.static import InputSpec
import paddle.optimizer as optimizer

def train(model):  
    start = time.perf_counter()
    # 初始化临时变量
    num_batch = 0
    best_result = 0
    best_result_id = 0
    elapsed = 0

    #Q6: 设计两层循环，分别实现根据周期循环和根据batch+_sizie循环，并在训练集上进行训练




    #Q7: 调用验证函数，实现对验证集的校验，并输出平均loss，top1精度和top5精度。同时要求将性能最好的模型进行保存到final_model_path




    print('训练完毕，最终性能accuracy={:.5f}(epoch={}), 总耗时{:.2f}s'.format(best_result, best_result_id, time.perf_counter() - start))

2.2.3 模型训练及在线测试

#### 训练主函数 ########################################################3
if __name__ == '__main__':

    # Q8：定义训练主函数，包括以下三个步骤：
    # 1. 设置输入样本的维度，包括对图像和标签的定义



    # 2. 实例化模型，并输入模型基本信息




    # 3. 设置学习率、优化器、损失函数和评价指标




    # 启动训练过程
    print('启动训练...')
    train(model)
    print('结果路径为 {}.'.format(final_models_path))

    模型参数信息：
    ---------------------------------------------------------------------------
     Layer (type)       Input Shape          Output Shape         Param #    
    ===========================================================================
       Linear-5         [[1, 30000]]           [1, 100]          3,000,100   
        ReLU-4           [[1, 100]]            [1, 100]              0       
       Linear-6          [[1, 100]]            [1, 256]           25,856     
        ReLU-5           [[1, 256]]            [1, 256]              0       
       Linear-7          [[1, 256]]            [1, 256]           65,792     
        ReLU-6           [[1, 256]]            [1, 256]              0       
       Linear-8          [[1, 256]]            [1, 10]             2,570     
    ===========================================================================
    Total params: 3,094,318
    Trainable params: 3,094,318
    Non-trainable params: 0
    ---------------------------------------------------------------------------
    Input size (MB): 0.11
    Forward/backward pass size (MB): 0.01
    Params size (MB): 11.80
    Estimated Total Size (MB): 11.93
    ---------------------------------------------------------------------------
    
    {'total_params': 3094318, 'trainable_params': 3094318}
    启动训练...
    Epoch:1/30, batch:10, train_loss:[4.39355], acc_top1:[0.07812], acc_top5:[0.42188](0.46s)
    Epoch:1/30, batch:20, train_loss:[2.74373], acc_top1:[0.07812], acc_top5:[0.40625](0.68s)
    [validation] Epoch:1/30, val_loss:[0.04341], val_top1:[0.10952], val_top5:[0.59048]
    最优top1测试精度:0.10952 (epoch=1)
    Epoch:2/30, batch:30, train_loss:[2.37259], acc_top1:[0.20312], acc_top5:[0.46875](1.33s)
    Epoch:2/30, batch:40, train_loss:[2.21174], acc_top1:[0.18750], acc_top5:[0.62500](0.41s)
    [validation] Epoch:2/30, val_loss:[0.04209], val_top1:[0.19524], val_top5:[0.70000]
    最优top1测试精度:0.19524 (epoch=2)
    Epoch:3/30, batch:50, train_loss:[2.22916], acc_top1:[0.15625], acc_top5:[0.59375](0.94s)
    Epoch:3/30, batch:60, train_loss:[2.04789], acc_top1:[0.21875], acc_top5:[0.75000](0.60s)
    [validation] Epoch:3/30, val_loss:[0.03844], val_top1:[0.28095], val_top5:[0.69048]
    最优top1测试精度:0.28095 (epoch=3)
    Epoch:4/30, batch:70, train_loss:[1.95388], acc_top1:[0.31250], acc_top5:[0.76562](1.34s)
    Epoch:4/30, batch:80, train_loss:[1.81739], acc_top1:[0.43750], acc_top5:[0.85938](0.46s)
    [validation] Epoch:4/30, val_loss:[0.03365], val_top1:[0.28095], val_top5:[0.80476]
    Epoch:5/30, batch:90, train_loss:[1.82858], acc_top1:[0.39062], acc_top5:[0.85938](0.58s)
    Epoch:5/30, batch:100, train_loss:[1.75928], acc_top1:[0.26562], acc_top5:[0.84375](0.57s)
    Epoch:5/30, batch:110, train_loss:[1.71472], acc_top1:[0.37500], acc_top5:[0.82812](0.44s)
    [validation] Epoch:5/30, val_loss:[0.02836], val_top1:[0.43333], val_top5:[0.84286]
    最优top1测试精度:0.43333 (epoch=5)
    Epoch:6/30, batch:120, train_loss:[1.34966], acc_top1:[0.53125], acc_top5:[0.93750](1.10s)
    Epoch:6/30, batch:130, train_loss:[1.70853], acc_top1:[0.25000], acc_top5:[0.90625](0.36s)
    [validation] Epoch:6/30, val_loss:[0.02931], val_top1:[0.44286], val_top5:[0.90952]
    最优top1测试精度:0.44286 (epoch=6)
    Epoch:7/30, batch:140, train_loss:[1.54897], acc_top1:[0.37500], acc_top5:[0.93750](0.83s)
    Epoch:7/30, batch:150, train_loss:[1.46881], acc_top1:[0.39062], acc_top5:[0.93750](0.46s)
    [validation] Epoch:7/30, val_loss:[0.02402], val_top1:[0.52857], val_top5:[0.93333]
    最优top1测试精度:0.52857 (epoch=7)
    Epoch:8/30, batch:160, train_loss:[1.26674], acc_top1:[0.54688], acc_top5:[0.95312](0.98s)
    Epoch:8/30, batch:170, train_loss:[1.41724], acc_top1:[0.46875], acc_top5:[0.93750](0.56s)
    [validation] Epoch:8/30, val_loss:[0.02306], val_top1:[0.57143], val_top5:[0.94762]
    最优top1测试精度:0.57143 (epoch=8)
    Epoch:9/30, batch:180, train_loss:[1.14159], acc_top1:[0.65625], acc_top5:[0.96875](0.90s)
    Epoch:9/30, batch:190, train_loss:[1.10799], acc_top1:[0.60938], acc_top5:[0.93750](0.55s)
    [validation] Epoch:9/30, val_loss:[0.02028], val_top1:[0.57619], val_top5:[0.96190]
    最优top1测试精度:0.57619 (epoch=9)
    Epoch:10/30, batch:200, train_loss:[1.23004], acc_top1:[0.56250], acc_top5:[0.93750](1.00s)
    Epoch:10/30, batch:210, train_loss:[1.08690], acc_top1:[0.59375], acc_top5:[0.93750](0.46s)
    Epoch:10/30, batch:220, train_loss:[0.87832], acc_top1:[0.73438], acc_top5:[0.96875](0.45s)
    [validation] Epoch:10/30, val_loss:[0.02122], val_top1:[0.60476], val_top5:[0.95238]
    最优top1测试精度:0.60476 (epoch=10)
    Epoch:11/30, batch:230, train_loss:[0.86703], acc_top1:[0.75000], acc_top5:[0.96875](0.77s)
    Epoch:11/30, batch:240, train_loss:[0.92345], acc_top1:[0.62500], acc_top5:[1.00000](0.56s)
    [validation] Epoch:11/30, val_loss:[0.03362], val_top1:[0.50476], val_top5:[0.93810]
    Epoch:12/30, batch:250, train_loss:[0.94919], acc_top1:[0.68750], acc_top5:[0.96875](0.76s)
    Epoch:12/30, batch:260, train_loss:[0.72333], acc_top1:[0.73438], acc_top5:[0.96875](0.45s)
    [validation] Epoch:12/30, val_loss:[0.02174], val_top1:[0.54762], val_top5:[0.95714]
    Epoch:13/30, batch:270, train_loss:[1.25069], acc_top1:[0.51562], acc_top5:[0.93750](0.56s)
    Epoch:13/30, batch:280, train_loss:[1.08153], acc_top1:[0.64062], acc_top5:[0.95312](0.54s)
    [validation] Epoch:13/30, val_loss:[0.02122], val_top1:[0.58571], val_top5:[0.94762]
    Epoch:14/30, batch:290, train_loss:[0.79241], acc_top1:[0.79688], acc_top5:[0.96875](0.56s)
    Epoch:14/30, batch:300, train_loss:[0.74392], acc_top1:[0.75000], acc_top5:[1.00000](0.46s)
    [validation] Epoch:14/30, val_loss:[0.01880], val_top1:[0.60476], val_top5:[0.96667]
    Epoch:15/30, batch:310, train_loss:[0.72252], acc_top1:[0.73438], acc_top5:[0.98438](0.48s)
    Epoch:15/30, batch:320, train_loss:[0.88343], acc_top1:[0.68750], acc_top5:[0.98438](0.44s)
    Epoch:15/30, batch:330, train_loss:[1.07243], acc_top1:[0.60938], acc_top5:[0.90625](0.55s)
    [validation] Epoch:15/30, val_loss:[0.01571], val_top1:[0.70952], val_top5:[0.97143]
    最优top1测试精度:0.70952 (epoch=15)
    Epoch:16/30, batch:340, train_loss:[0.96580], acc_top1:[0.70312], acc_top5:[0.96875](0.77s)
    Epoch:16/30, batch:350, train_loss:[0.69921], acc_top1:[0.78125], acc_top5:[0.95312](0.65s)
    [validation] Epoch:16/30, val_loss:[0.01652], val_top1:[0.69048], val_top5:[0.95714]
    Epoch:17/30, batch:360, train_loss:[1.27291], acc_top1:[0.53125], acc_top5:[0.92188](0.46s)
    Epoch:17/30, batch:370, train_loss:[0.61907], acc_top1:[0.78125], acc_top5:[1.00000](0.65s)
    [validation] Epoch:17/30, val_loss:[0.01634], val_top1:[0.73333], val_top5:[0.96190]
    最优top1测试精度:0.73333 (epoch=17)
    Epoch:18/30, batch:380, train_loss:[0.81712], acc_top1:[0.70312], acc_top5:[1.00000](0.88s)
    Epoch:18/30, batch:390, train_loss:[0.55936], acc_top1:[0.82812], acc_top5:[0.98438](0.55s)
    [validation] Epoch:18/30, val_loss:[0.01569], val_top1:[0.70000], val_top5:[0.95714]
    Epoch:19/30, batch:400, train_loss:[0.70603], acc_top1:[0.70312], acc_top5:[0.95312](0.59s)
    Epoch:19/30, batch:410, train_loss:[0.88434], acc_top1:[0.64062], acc_top5:[0.98438](0.45s)
    [validation] Epoch:19/30, val_loss:[0.01592], val_top1:[0.69524], val_top5:[0.96190]
    Epoch:20/30, batch:420, train_loss:[0.72619], acc_top1:[0.78125], acc_top5:[0.93750](0.68s)
    Epoch:20/30, batch:430, train_loss:[0.68058], acc_top1:[0.76562], acc_top5:[0.98438](0.44s)
    Epoch:20/30, batch:440, train_loss:[0.84574], acc_top1:[0.68750], acc_top5:[0.98438](0.44s)
    [validation] Epoch:20/30, val_loss:[0.02193], val_top1:[0.61429], val_top5:[0.96667]
    Epoch:21/30, batch:450, train_loss:[1.09199], acc_top1:[0.65625], acc_top5:[0.92188](0.56s)
    Epoch:21/30, batch:460, train_loss:[0.76067], acc_top1:[0.76562], acc_top5:[0.96875](0.55s)
    [validation] Epoch:21/30, val_loss:[0.01762], val_top1:[0.66667], val_top5:[0.96667]
    Epoch:22/30, batch:470, train_loss:[0.63677], acc_top1:[0.68750], acc_top5:[0.98438](0.57s)
    Epoch:22/30, batch:480, train_loss:[0.52120], acc_top1:[0.79688], acc_top5:[0.98438](0.44s)
    [validation] Epoch:22/30, val_loss:[0.01756], val_top1:[0.67619], val_top5:[0.94286]
    Epoch:23/30, batch:490, train_loss:[0.32460], acc_top1:[0.87500], acc_top5:[1.00000](0.67s)
    Epoch:23/30, batch:500, train_loss:[0.64572], acc_top1:[0.76562], acc_top5:[0.98438](0.55s)
    [validation] Epoch:23/30, val_loss:[0.02536], val_top1:[0.57619], val_top5:[0.94762]
    Epoch:24/30, batch:510, train_loss:[0.40627], acc_top1:[0.84375], acc_top5:[1.00000](0.46s)
    Epoch:24/30, batch:520, train_loss:[0.64004], acc_top1:[0.78125], acc_top5:[0.96875](0.45s)
    [validation] Epoch:24/30, val_loss:[0.01460], val_top1:[0.72381], val_top5:[0.96190]
    Epoch:25/30, batch:530, train_loss:[0.57668], acc_top1:[0.76562], acc_top5:[1.00000](0.68s)
    Epoch:25/30, batch:540, train_loss:[0.91435], acc_top1:[0.68750], acc_top5:[1.00000](0.56s)
    Epoch:25/30, batch:550, train_loss:[0.54931], acc_top1:[0.79688], acc_top5:[0.98438](0.44s)
    [validation] Epoch:25/30, val_loss:[0.01700], val_top1:[0.66190], val_top5:[0.95714]
    Epoch:26/30, batch:560, train_loss:[0.39254], acc_top1:[0.84375], acc_top5:[1.00000](0.58s)
    Epoch:26/30, batch:570, train_loss:[0.32121], acc_top1:[0.92188], acc_top5:[1.00000](0.55s)
    [validation] Epoch:26/30, val_loss:[0.01788], val_top1:[0.71905], val_top5:[0.96667]
    Epoch:27/30, batch:580, train_loss:[0.43097], acc_top1:[0.85938], acc_top5:[1.00000](0.50s)
    Epoch:27/30, batch:590, train_loss:[0.82380], acc_top1:[0.67188], acc_top5:[0.98438](0.55s)
    [validation] Epoch:27/30, val_loss:[0.01630], val_top1:[0.68571], val_top5:[0.96667]
    Epoch:28/30, batch:600, train_loss:[1.02327], acc_top1:[0.64062], acc_top5:[0.98438](0.58s)
    Epoch:28/30, batch:610, train_loss:[0.29247], acc_top1:[0.92188], acc_top5:[1.00000](0.35s)
    [validation] Epoch:28/30, val_loss:[0.01566], val_top1:[0.71905], val_top5:[0.97619]
    Epoch:29/30, batch:620, train_loss:[0.59154], acc_top1:[0.75000], acc_top5:[1.00000](0.76s)
    Epoch:29/30, batch:630, train_loss:[0.43663], acc_top1:[0.85938], acc_top5:[1.00000](0.45s)
    [validation] Epoch:29/30, val_loss:[0.02399], val_top1:[0.56667], val_top5:[0.94762]
    Epoch:30/30, batch:640, train_loss:[0.42324], acc_top1:[0.87500], acc_top5:[0.98438](0.78s)
    Epoch:30/30, batch:650, train_loss:[0.42873], acc_top1:[0.89062], acc_top5:[0.98438](0.55s)
    Epoch:30/30, batch:660, train_loss:[0.73652], acc_top1:[0.73438], acc_top5:[0.98438](0.35s)
    [validation] Epoch:30/30, val_loss:[0.01745], val_top1:[0.69048], val_top5:[0.96190]
    训练完毕，最终性能accuracy=0.73333(epoch=17), 总耗时40.19s
    结果路径为 D:\Workspace\ExpResults\Project007FFNGestures\final_model.

需要注意的是，以上训练过程是基于随机初始化后的优化过程，因此每次训练获得的结果通常是不相同的，但最终收敛后的结果是近似相等的。

2.3 离线测试

if __name__ == '__main__':
    # Q9：调用训练好的模型，分别在验证集和测试集上进行测试，包括以下三个步骤
    # 1. 设置输入样本的维度    
    input_spec = InputSpec(shape=[None, 3*100*100], dtype='float32', name='image')
    label_spec = InputSpec(shape=[None, 1], dtype='int64', name='label')
    
    # 2. 载入模型
                                                                            # 模型实例化 
                                                                            # 模型初始化
                                                                            # 载入调优模型的参数
                                                                            # 设置loss
                                                                            # 设置评价指标
    
    # 3. 执行评估函数，并输出验证集样本的损失和精度
    print('开始评估...')
                                                                            # 对验证集进行评估
    print('\r [验证集] 损失: {:.5f}, top1精度:{:.5f}, top5精度为:{:.5f} \n'.format(avg_loss, avg_acc_top1, avg_acc_top5), end='')    
                                                                            # 对测试集进行评估
    print('\r [测试集] 损失: {:.5f}, top1精度:{:.5f}, top5精度为:{:.5f}'.format(avg_loss, avg_acc_top1, avg_acc_top5), end='')

开始评估...
[验证集] 损失: 0.01634, top1精度:0.73333, top5精度为:0.96190
[测试集] 损失: 0.01533, top1精度:0.70952, top5精度为:0.96429

【实验三】模型评估与推理(应用)

实验难度：中等
实验摘要：从硬盘载入已经训练好的多层感知机模型，实现对给定图像的推理和预测。
实验目标：
1. 学会载入已训练好的模型
2. 掌握模型的验证与推理方法
3. 学会对图像根据需要进行预处理，包括尺度变换，像素值归一化，数据形态变换
实验建议：
1. 特别注意推理时所使用的数据预处理应该和训练时的完全一致。
2. 理解推理模型和调优模型的区别，并且根据需要选择不同的模型载入方法。例如此处所用的推理模型应该使用paddle.jit.load()进行模型载入。
3. 与训练类似，推理部分包含三个部分：导入依赖库及全局参数配置、获取待预测数据并进行预处理、载入模型并开始进行预测。

3.1 导入依赖库及全局参数配置

# 导入依赖库
import os
import cv2
import numpy as np
import paddle                      # 载入PaddlePaddle基本库
import matplotlib.pyplot as plt    # 载入python的第三方图像处理库

# 设置载入模型，此处我们调用训练中获得的最好的一个模型
project_name      = 'Project007FFNGestures'
result_root_path  = 'D:\\Workspace\\ExpResults\\'
final_models_path = os.path.join(result_root_path, project_name, 'final_model')

3.2 获取待预测数据

获取待测数据包含两个步骤: 读取待测图像和图像预处理。函数 load_image() 实现从指定位置读取待测图像, 并对该图像进行预处理。此处的预处理方案和训练模型时所使用的预处理方案必须是一致的。

首先需要将所有样本都resize到同样的尺度；
将图像数据转换为numpy.array格式, 32bit浮点数据类型(float32)；
将像素值的取值范围调整为:0-1, 原始范围为:0-255；
将图像转换为Paddle内部的Tensor格式；
对于多层感知机，还需要将图像转换为向量形式。

import paddle.vision.transforms as T

#Q10. 读取预测图像并进行预处理，注意和训练集的处理方法保持一致
def load_image(img_path):
    img =                                           # 以RGB模式读取图像
    img =                                           # 将图像尺度resize为指定尺寸
    img =                                           # 将图像数据类型转化为float32
    img =                                           # 将像素值归一化到[0,1]之间

    transforms = T.ToTensor()      
    img =                                           # 调整数据形状paddle默认格式
    img =                                           # 将图像拉伸成向量

    return img

3.3 载入模型并开始进行预测

import random
i = random.randint(0,9)         
img_path = 'D:\\Workspace\\ExpDatasets\\Gestures\\Infer\\infer_' + str(i) + '.jpg'  # 从预先准备的推理图像文件中随机抽取一幅图像，该文件夹中包含0-9共10个示例图片
# img_path = 'D:\\Workspace\\ExpDatasets\\Gestures\\Infer\\infer_9.jpg'             # 手动指定一张图片进行推理测试

# Q11： 使用训练好的模型对给定的图像进行推理，包括以下三个步骤：
# 1. 载入推理模型并进行实例化
model = 

# 2. 载入待预测图像
img = 

# 3. 使用模型进行前向推理
logits = 
pred = 
print('手势文件 {} 的标签为: {}, 预测结果为: {}'.format(os.path.basename(img_path), os.path.basename(img_path)[-5], pred))

# 4. 输出图像文件
image = cv2.imread(img_path, 1)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
plt.imshow(image)

手势文件 infer_5.jpg 的标签为: 5, 预测结果为: 5
<matplotlib.image.AxesImage at 0x19834ec5fd0>
output_28_2

【项目007】基于多层感知机的手势识别（学生版） 显示答案 | 返回首页