【项目006】基于线性回归的波士顿房价预测隐藏答案 | 返回首页

作者：欧新宇（Xinyu OU）
当前版本：Release v1.0
开发平台：Paddle 2.5.2
运行环境：Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案所涉及的数据集仅用于教学和交流使用，请勿用作商用。

最后更新：2024年5月30日

经典的线性回归模型主要用来预测一些存在着线性关系的数据。回归模型可以理解为：存在一个点集，用一条曲线去拟合它分布的过程。如果拟合曲线是一条直线，则称为 线性回归。如果是一条二次曲线，则被称为 二次回归。线性回归是回归模型中最简单的一种。

在本项目中，我们使用飞桨Paddle框架来实现波士顿房价（UCIHousing）预测。其思路是，假设uci-housing 数据集中的房子属性和房价之间的关系可以被属性间的线性组合描述。

在模型训练阶段，让假设的预测结果和真实值之间的误差越来越小。
在模型预测阶段，预测器会读取训练好的模型，对从未遇见过的房子属性进行房价预测。

【实验说明】

一、实验目的

掌握线性回归模型的基本原理。
掌握线性回归模型的基本用法。
掌握线性回归模型的基本训练过程。
掌握线性回归模型的基本预测过程。

二、实验要求

所有作业均在AIStudio上进行提交，提交时包含源代码及运行结果
Q1: 补全代码，实现必要库的导入及根目录的定义（10分）
Q2-1：补全数据集路径的定义代码(10分)
Q2-2：补全代码，将数据形状调整为指定形态（10分）
Q2-3：补全下代码，完成数据的归一化处理（10分）
Q3-1：补全代码，完成模型的定义（10分）
Q3-2：补全代码，完成模型训练（20分）
Q4-1：补全代码，完成模型推理（20分）
Q4-2：补全代码，完成模型评价（10分）

三、思维导图

四、目录结构

本项目目录结构说明（可根据实际情况进行修改）
- 数据集根目录：
  - Windows: D:\WorkSpace\ExpDatasets\UCIHousing\housing.data
  - AIStudio: /home/aistudio/work/data295069/housing.data

【实验一】环境配置

实验摘要： 在深度学习的应用中，环境配置是至关重要的，它包括各种重要的库的载入，常用路径的指定，以及基本参数的配置。预先进行统一定义，而不是在每次使用时都进行配置，可以大大提高工作效率。此外，在正式的项目开发和部署中，这些环境的配置可以通过配置文件进行统一管理。

实验目的：

学会配置程序运行所需要的基本库
学会定义项目运行需要的常用路径，具体包括输入的路径和输出的路径，本项目只需要定义初始根目录。

# Q1: 补全以下代码，实现必要库的导入及根目录的定义
# [Your codes 1]
import paddle                           # 导入飞桨paddle库
import numpy as np                      # 导入NumPy库，用于数据处理
import os                               # 导入系统库，用于处理系统路径
import matplotlib.pyplot as plt         # 导入matplotlib绘图库，用于数据可视化
import pandas as pd                     # 导入pandas库，用于数据分析和处理
import seaborn as sns                   # 导入seaborn绘图库，用于数据可视化
import warnings                         # 导入警告库，用于忽略警告信息（非必须）
warnings.filterwarnings("ignore")

# print(paddle.__version__)

# 1. 基本路径的定义 
# root_path = 'D:\\WorkSpace\\'           # 定义项目根目录
root_path = '/home/aistudio/'             # 定义项目根目录

# 2. 基本参数的定义（本例略）

【实验二】数据集载入和预处理

实验摘要： 几乎所有的深度学习任务都有一个特点，就是需要大量的数据，也就是我们常说的数据驱动。在深度学习模型训练之前，我们通常需要对数据进行预处理，虽然针对不同的数据集预处理的方法和目标不一定相同，但总的来说它们包括数据清洗，数据转换，数据归一化，数据列表划分等几个部分，此外为了较好实现这些功能，通常还需要对数据进行可视化以便于选择合适的处理方法。本实验也将包含以上几个步骤。

实验目的：

学会从文件中读取数据集
学会对数据进行清洗，转换，归一化，划分等预处理操作
学会对数据进行可视化，以便于选择合适的预处理方法

2.0 Seaborn 库的安装

在本实验中，我们需要使用一个第三方的数据可视化库Seaborn，该库通常包含于Anaaconda包中，在本地运行的时候可以不进行额外安装。但由于AIStudio并没有内置该库，因此需要使用如下命令进行手动安装。

!python -m pip install seaborn

Looking in indexes: https://mirror.baidu.com/pypi/simple/, https://mirrors.aliyun.com/pypi/simple/
Collecting seaborn
  Downloading https://mirrors.aliyun.com/pypi/packages/83/11/00d3c3dfc25ad54e731d91449895a79e4bf2384dc3ac01809010ba88f6d5/seaborn-0.13.2-py3-none-any.whl (294 kB)
     ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 294.9/294.9 kB 4.0 MB/s eta 0:00:00a 0:00:01
Requirement already satisfied: numpy!=1.24.0,>=1.20 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from seaborn) (1.26.4)
Requirement already satisfied: pandas>=1.2 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from seaborn) (2.2.2)
Requirement already satisfied: matplotlib!=3.6.1,>=3.4 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from seaborn) (3.9.1)
Requirement already satisfied: contourpy>=1.0.1 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from matplotlib!=3.6.1,>=3.4->seaborn) (1.2.1)
Requirement already satisfied: cycler>=0.10 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from matplotlib!=3.6.1,>=3.4->seaborn) (0.12.1)
Requirement already satisfied: fonttools>=4.22.0 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from matplotlib!=3.6.1,>=3.4->seaborn) (4.53.0)
Requirement already satisfied: kiwisolver>=1.3.1 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from matplotlib!=3.6.1,>=3.4->seaborn) (1.4.5)
Requirement already satisfied: packaging>=20.0 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from matplotlib!=3.6.1,>=3.4->seaborn) (24.1)
Requirement already satisfied: pillow>=8 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from matplotlib!=3.6.1,>=3.4->seaborn) (10.4.0)
Requirement already satisfied: pyparsing>=2.3.1 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from matplotlib!=3.6.1,>=3.4->seaborn) (3.1.2)
Requirement already satisfied: python-dateutil>=2.7 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from matplotlib!=3.6.1,>=3.4->seaborn) (2.9.0.post0)
Requirement already satisfied: pytz>=2020.1 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from pandas>=1.2->seaborn) (2024.1)
Requirement already satisfied: tzdata>=2022.7 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from pandas>=1.2->seaborn) (2024.1)
Requirement already satisfied: six>=1.5 in /opt/conda/envs/python35-paddle120-env/lib/python3.10/site-packages (from python-dateutil>=2.7->matplotlib!=3.6.1,>=3.4->seaborn) (1.16.0)
Installing collected packages: seaborn
Successfully installed seaborn-0.13.2
WARNING: Skipping page https://mirror.baidu.com/pypi/simple/pip/ because the GET request got Content-Type: application/octet-stream. The only supported Content-Types are application/vnd.pypi.simple.v1+json, application/vnd.pypi.simple.v1+html, and text/html

2.1 数据集介绍

本项目所采用的 uci-housing数据集，这经典线性回归的数据集，它包含7084条列表数据。这些数据被分为506组，每组数据表示一幢房子，每幢房子都有14个属性，其中前13列用来描述房屋的各种信息，最后一列为该类房屋价格中位数。

属性名	介绍
CRIM	城镇人均犯罪率
ZN	住宅用地超过25000平方英尺的比例
INDUS	非零售业务用地的比例
CHAS	是否邻近 Charles River（重要属性，1表示邻近，0表示不邻近）
NOX	一氧化氮浓度
RM	住宅平均客房数
AGE	1940年之前建成的自用单位比例
DIS	到波士顿五个就业中心的加权距离
RAD	到径向公路的可达性指数
TAX	每1000美元的全值财产税率
PTRATIO	所在区域师生比例
B	1000(Bk - 0.63) $^2$ ，其中Bk是城镇黑人的比例
LSTAT	低收入人群占比
MEDV	同类房屋价格的中位数

2.2 数据集载入

数据集载入是深度学习模型训练和预测的基础，它包括从文件中读取数据集，并将其转换为模型训练和预测所需要的形式。

# Q2-1：补全以下数据集路径的定义代码
# [Your codes 2]
# 1. 从文件导入数据
dataset_path = os.path.join(root_path, 'ExpDatasets', 'UCIHousing', 'housing.data')    # Windows
# dataset_path = os.path.join(root_path, 'data', 'data295069', 'housing.data')    # AIStudio

# 2. 将空格作为分割符来对数据进行拆分（可以先使用vscode等工具先打开文件观察后再确定分割符）
housing_data = np.fromfile(dataset_path, sep=' ')

# 3. 根据数据集的描述设置特征的名称
feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
feature_num = len(feature_names)

# Q2-2：补全以下代码，将数据形状调整为指定形态
# [Your codes 3]
# 4. 将原始数据进行Reshape，目标形状为 [N, 14] 的数据
housing_data = housing_data.reshape([housing_data.shape[0] // feature_num, feature_num])

2.3 数据分析及归一化处理

2.3.1 列表分析：使用pandas库将数据进行可视化

# 画图看特征间的关系,主要是变量两两之间的关系（线性或非线性，有无明显较为相关关系）
features_np = np.array([x[:13] for x in housing_data], np.float32)
labels_np = np.array([x[-1] for x in housing_data], np.float32)
# data_np = np.c_[features_np, labels_np]
df = pd.DataFrame(housing_data, columns=feature_names)
df

-	CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT	MEDV
0	0.00632	18.0	2.31	0.0	0.538	6.575	65.2	4.0900	1.0	296.0	15.3	396.90	4.98	24.0
1	0.02731	0.0	7.07	0.0	0.469	6.421	78.9	4.9671	2.0	242.0	17.8	396.90	9.14	21.6
2	0.02729	0.0	7.07	0.0	0.469	7.185	61.1	4.9671	2.0	242.0	17.8	392.83	4.03	34.7
3	0.03237	0.0	2.18	0.0	0.458	6.998	45.8	6.0622	3.0	222.0	18.7	394.63	2.94	33.4
4	0.06905	0.0	2.18	0.0	0.458	7.147	54.2	6.0622	3.0	222.0	18.7	396.90	5.33	36.2
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
501	0.06263	0.0	11.93	0.0	0.573	6.593	69.1	2.4786	1.0	273.0	21.0	391.99	9.67	22.4
502	0.04527	0.0	11.93	0.0	0.573	6.120	76.7	2.2875	1.0	273.0	21.0	396.90	9.08	20.6
503	0.06076	0.0	11.93	0.0	0.573	6.976	91.0	2.1675	1.0	273.0	21.0	396.90	5.64	23.9
504	0.10959	0.0	11.93	0.0	0.573	6.794	89.3	2.3889	1.0	273.0	21.0	393.45	6.48	22.0
505	0.04741	0.0	11.93	0.0	0.573	6.030	80.8	2.5050	1.0	273.0	21.0	396.90	7.88	11.9

506 rows × 14 columns

2.3.2 可视化分析

sns.pairplot(df, y_vars=feature_names[-1], x_vars=feature_names[0:5], dropna=True)
sns.pairplot(df, y_vars=feature_names[-1], x_vars=feature_names[5:10], dropna=True)
sns.pairplot(df, y_vars=feature_names[-1], x_vars=feature_names[10::], dropna=True)
plt.show()

# dropna=True: 删除包含缺失值的行

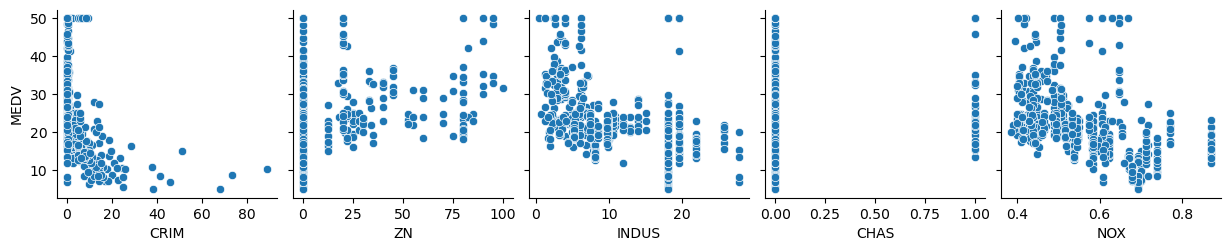
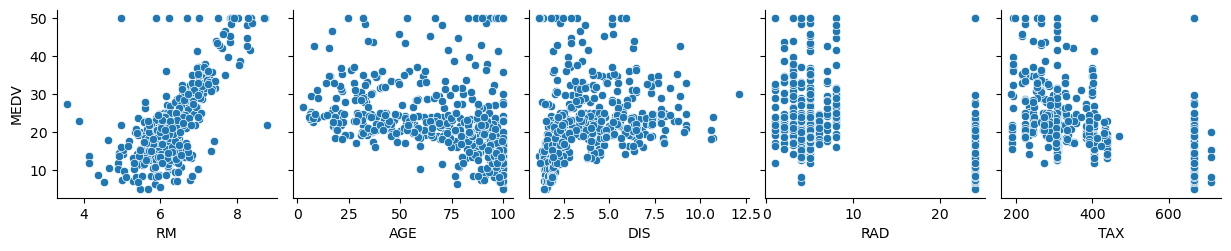
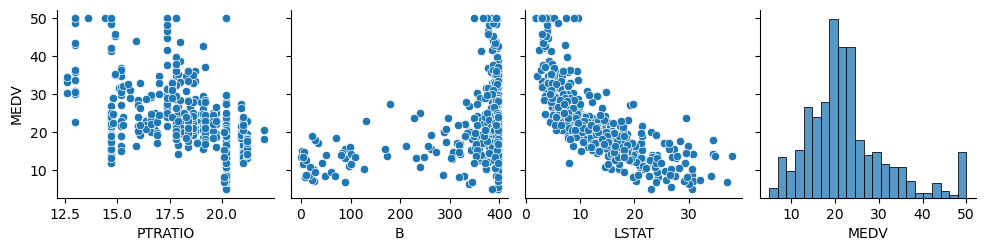
2.3.3 相关性分析

fig, ax = plt.subplots(figsize=(15, 1)) 
corr_data = df.corr().iloc[-1]
corr_data = np.asarray(corr_data).reshape(1, 14)
ax = sns.heatmap(corr_data, annot=True, cmap='Blues')
plt.show()

2.3.4 数据归一化处理

对于表格数据来说，有时候数据可能因为表达方式的不同而存在量纲差异，比如一个数据集的取值范围在0-1000，而另一个数据集的取值范围在0-1000000，这样在计算损失时，数据量纲差异会使得模型训练变得困难。因此，在进行模型训练之前，我们需要对数据进行归一化处理。下图给出本数据集中各属性的取值范围分布：

plt.figure(figsize=(6, 3))
sns.boxplot(data=df.iloc[:, 0:13])

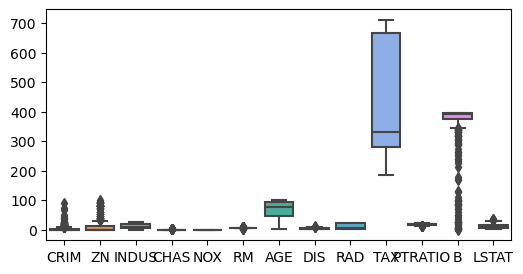
从上图可以看出，13种属性的数值范围差异太大，特别是 tax 属性的取值与其他属性存在较大差异，此时展示出来的分布情况呈明显偏离。同时，由于该属性取值较大，导致 CHAS, NOX, RM 等属性的最大、最小值以及异常值已经无法正常显示。此时，我们需要对原始数据进行归一化处理，以确保数据的量纲保持一致。

一般来说，归一化（或 Feature scaling） 至少有以下2个理由：

过大或过小的数值范围会导致计算时的浮点上溢或下溢。
不同的数值范围会导致不同属性对模型的重要性不同（至少在训练的初始阶段如此），而这个隐含的假设常常是不合理的。这会对优化的过程造成困难，使训练时间大大地加长.

下面我们使用 平均归一化 对数据集进行归一化处理，其基本公式如下：
$X_{norm}=\frac{X-\mu}{\max - \min}$

其中， $X$ 表示原始数据集， $\mu$ 表示均值， $\max, \min$ 表示标准差。

# Q2-3：补全以下代码，完成数据的归一化处理
# [Your codes 4]

# 1. 计算最大值、最小值和均值
features_max = housing_data.max(axis=0)
features_min = housing_data.min(axis=0)
features_avg = housing_data.sum(axis=0) / housing_data.shape[0]

# 2. 按batch_size进行归一化
batch_size = 10
def feature_norm(input):
    f_size = input.shape
    output_features = np.zeros(f_size, np.float32)
    for batch_id in range(f_size[0]):
        for index in range(13):
            output_features[batch_id][index] = (input[batch_id][index] - features_avg[index]) / (features_max[index] - features_min[index])
    return output_features

# 3. 对属性进行归一化处理
housing_features_norm = feature_norm(housing_data[:, :13])
housing_data_norm = np.c_[housing_features_norm, housing_data[:, -1]].astype(np.float32)
df_norm = pd.DataFrame(housing_data_norm, columns=feature_names)

下面我们对比归一化前后的数据分布情况，可以发现，归一化后的数据分布情况已经非常接近正态分布，几乎都满足于均值为0，标准差为1。

# 4. 可视化分析（量纲对比）
plt.figure(figsize=(12, 3))
plt.subplot(1,2,1)
sns.boxplot(df.iloc[:, 0:13])
plt.title('origin data')
plt.subplot(1,2,2)
sns.boxplot(df_norm.iloc[:, 0:13])
plt.title('regularized data')

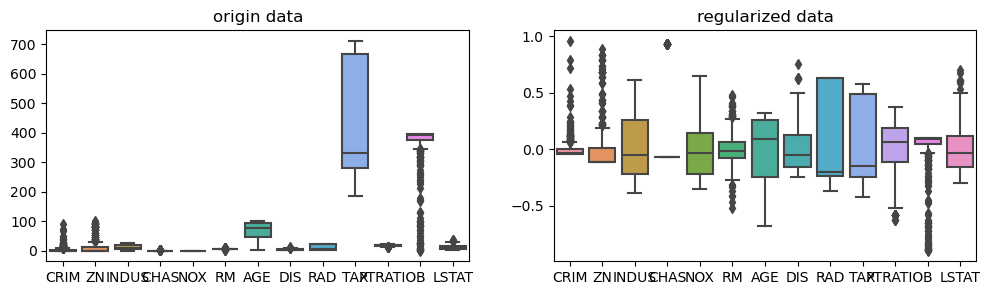
2.4 数据划分

对于一个完整的数据集，通常需要划分为：训练集、验证集和测试集三个部分。其中，训练集用于模型的训练，验证集用于模型的选择，测试集用于模型的评估。在本例中，为了简便，我们仅使用训练集+测试集的划分方法，在后续的项目中我们会按照更标准的三类进行划分。对于比较简单的数据，可以使用 sklearn 库中的 train_test_split() 方法进行数据集划分，该方法接收以下参数：

X: 特征数据集
y: 标签数据集
test_size: 测试集所占比例
random_state: 随机数种子，用于保证每次划分的结果一致

此处，我们可以将数据集按照8:2的比例划分为训练集和测试集，分别用于训练和预测。这里我们使用 sklearn 库中的 train_test_split() 方法进行数据集划分，但实际使用中也可以手动进行划分，但应注意需要先将数据列表进行打乱。

数据划分之后，我们还需要创建一个数据读取器，用于将训练数据和测试数据封装成 paddle.io.Dataset 类型的数据集和 paddle.io.DataLoader 数据迭代读取器，方便后续的模型训练和预测。

import paddle.io
from sklearn.model_selection import train_test_split
# 1. 数据划分
train_data, test_data = train_test_split(housing_data_norm, test_size=0.2)

# 2. 生成train和test数据迭代读取器
train_reader = [train_data[k: k+batch_size] for k in range(0, len(train_data), batch_size)]
test_reader = [test_data[k: k+batch_size] for k in range(0, len(test_data), batch_size)]

######################################################################################
# 测试读取器
if __name__ == "__main__":
    for i, data in enumerate(test_reader):
        features = data[:, :13]
        labels = data[:, -1]
        if i == 2:
            break
        print('验证集batch_{}的图像形态:{}, 标签形态:{}'.format(i, features.shape, labels.shape))

验证集batch_0的图像形态:(10, 13), 标签形态:(10,)
验证集batch_1的图像形态:(10, 13), 标签形态:(10,)

【实验三】模型定义及训练

实验摘要： 模型定义、训练及评估是深度学习的核心，也是深度学习应用的基础。本实验将介绍如何定义一个最简单的线性回归，并使用训练数据对模型进行训练，在后面更复杂的项目中，我们还将通过验证数据在训练的过程中进行模型的验证评估。此外，在训练中，为了便于了解训练的过程，我们会分别文本显示训练过程的示例和图像显示训练过程的示例。

实验目的：

学会使用paddle.nn.Layer定义一个深度学习模型
学会定义训练函数来对模型进行训练
学会定义可视化函数来显示和分析训练过程
学会定义日志显示语句来显示和分析训练过程

3.1 模型定义

在深度学习模型中，通常需要定义一个继承自 paddle.nn.Layer 的类，并重写 __init__() 和 forward() 函数。其中，__init__() 函数用于定义模型的参数，forward() 函数用于定义模型的前向传播过程。在 __init__() 函数中，我们通常会定义模型的参数，例如：全连接层的输入和输出维度、卷积层的卷积核个数、卷积核的大小等。在 forward() 函数中，我们通常会定义模型的前向传播过程，例如：全连接层的线性变换、卷积层的卷积操作等。

在本例中，我们只需要定义一个全连接层，用于将输入的13维特征数据转换为1维的预测结果。在定义模型时，我们通常会使用 paddle.nn.Linear 函数来定义这个全连接层。此外，我们通常可以使用Paddle自带的模型打印函数 paddle.summary() 来输出模型的结构，以判断模型的定义是否正确。

# Q3-1：补全以下代码，完成模型的定义
# [Your codes 5]

class LinearRegressor(paddle.nn.Layer):
    def __init__(self, num_classes=13):
        super().__init__()
        self.features = paddle.nn.Linear(num_classes, 1,)

    def forward(self, inputs):
        pred = self.features(inputs)
        return pred
    
model = LinearRegressor()               # 创建模型实例
paddle.summary(model, (64, 13))         # 测试模型

---------------------------------------------------------------------------
 Layer (type)       Input Shape          Output Shape         Param #    
===========================================================================
   Linear-3          [[64, 13]]            [64, 1]              14       
===========================================================================
Total params: 14
Trainable params: 14
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.00
Params size (MB): 0.00
Estimated Total Size (MB): 0.00
---------------------------------------------------------------------------
{'total_params': 14, 'trainable_params': 14}

3.2 定义训练过程的损失值可视化函数

在训练过程中，通常会使用一些可视化方法来了解训练过程的损失和精度变化情况，以便于对训练的超参数进行定义，并分析训练的正确性。值得注意的是, 训练过程中可以每个epoch绘制一个数据点，也可以每个batch绘制一个数据点，也可以每个n个batch或n个epoch绘制一个数据点。这里我们按照每个iteration（batch）绘制一个数据点。在本项目中，我们将模型迭代次数及训练损失作为参数输入到可视化函数中。

def draw_train_process(iters, train_loss):
    plt.figure(figsize=(4, 3))
    plt.title("training loss")
    plt.xlabel("iter")
    plt.ylabel("loss")
    plt.plot(iters, train_loss, color='red', label='train_loss')
    plt.show()

3.3 模型训练

这里使用线性回归模型最常用的损失函数–均方误差（MSE），用来衡量模型预测的房价和真实房价的差异。对损失函数进行优化所采用的方法是梯度下降法。模型的训练过程由两层循环实现，第一层循环控制训练的轮数，第二层循环控制每个batch的训练。在每一轮训练中，模型会基于当前的参数计算预测结果和损失，并使用损失函数计算损失值，然后使用梯度下降法更新参数，直到损失值不再减小。在训练过程中，我们通常会每隔一定轮数打印一次损失值，以了解训练的进度。

import paddle.optimizer as optimizer
import paddle.nn.functional as F

train_nums = []
train_loss = []
def train(model):
    model.train()
    EPOCH_NUM = 200
    optimizer = paddle.optimizer.SGD(learning_rate=0.001, parameters=model.parameters())

    print('启动训练...')
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_reader):
            features = paddle.to_tensor(data[:, :13])
            labels = paddle.to_tensor(data[:, -1:])
            y_pred = model(features)
            avg_loss = F.mse_loss(y_pred, labels)
            avg_loss.backward()
            optimizer.minimize(avg_loss)
            model.clear_gradients()

        train_nums.append(epoch_id)
        train_loss.append(avg_loss)
        if epoch_id % 20 == 0:
            print("epoch: {}, loss: {}".format(epoch_id, avg_loss.numpy()))
    print('训练结束!')

model = LinearRegressor()
train(model)

启动训练...
epoch: 0, loss: [460.7455]
epoch: 20, loss: [48.82269]
epoch: 40, loss: [22.60188]
epoch: 60, loss: [17.231092]
epoch: 80, loss: [14.856593]
epoch: 100, loss: [13.338692]
epoch: 120, loss: [12.167496]
epoch: 140, loss: [11.185765]
epoch: 160, loss: [10.332624]
epoch: 180, loss: [9.578196]
训练结束!

3.4 调用可视化函数显示训练损失曲线

draw_train_process(train_nums, train_loss)

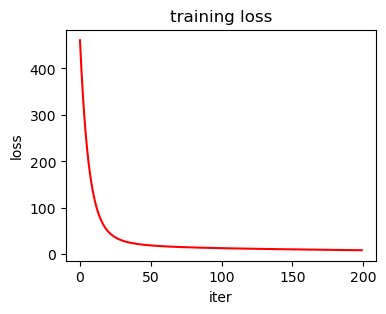
可以从上图看出，随着训练轮次的增加，损失在呈降低趋势。但由于每次仅基于少量样本更新参数和计算损失，所以损失下降曲线会出现震荡。

【实验四】模型的推理和预测

实验摘要： 模型推理和预测是深度学习应用的核心，也是深度学习应用的最终目的。本实验将介绍如何使用训练好的模型对测试数据进行推理和预测。

实验目的：

学会使用paddle.to_tensor()函数将数据转换为tensor格式
学会使用paddle.concat()函数将多个tensor拼接在一起
学会使用paddle.mean()函数计算tensor的平均值
学会使用paddle.pow()函数计算tensor的平方
学会根据需要对模型结果进行可视化分析

test_preds = paddle.to_tensor([])
test_labels = paddle.to_tensor([])

sum_cost = 0
# Q4-1：补全以下代码，完成模型推理
# [Your codes 7]
# 1. 对测试数据进行前向传播获得预测结果
for batch_id, data in enumerate(test_reader):                      # 遍历测试数据
    test_feature = paddle.to_tensor(data[:, :13])                  # 将数据转换为tensor格式
    test_label = paddle.to_tensor(data[:, -1])                     # 将数据转换为tensor格式
    test_pred = model(test_feature)                                # 使用模型将测试数据进行前向传播

    test_preds = paddle.concat(x = [test_preds, test_pred])        # 将每个batch的预测结果拼接在一起
    test_labels = paddle.concat(x = [test_labels, test_label])     # 将每个batch真实标签拼接在一起

# 2. 计算测试数据的预测结果与真实结果的均方误差
# Q4-2：补全以下代码，完成模型评价
# [Your codes 8]
cost = paddle.pow(test_preds - test_labels, 2) / 2
mean_loss = paddle.mean(cost).numpy()
print("MSE loss: {:.2f}". format(mean_loss[0]))

MSE loss: 58.78

下面我们给出预测结果的可视化，第一个图展示了预测结果拟合的曲线与真实离散数据的对比，第二个图展示了预测结果与真实结果的散点图的拟合关系。

def plot_pred_ground(pred, ground):
    plt.figure(figsize=(10, 8)) 
    plt.subplot(2,1,1)
    x_label = np.linspace(0, 101, 102)
    plt.scatter(x_label, pred, alpha=0.5, label='GrandTruth')  #  scatter:散点图, alpha:"透明度"
    plt.plot(x_label, ground, c='red', label='Prediction')  
    plt.title("The curve of predicted discrete points")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.legend()
    plt.subplot(2,1,2)
    plt.scatter(ground, pred, alpha=0.5, label='GrandTruth')  #  scatter:散点图, alpha:"透明度"
    plt.plot(ground, ground, c='red', label='Prediction')  
    plt.title("The linear regression curve")
    plt.xlabel("ground truth price(unit:$1000)")
    plt.ylabel("predict price")
    plt.legend()
    plt.subplots_adjust(hspace=0.3)
    plt.show()
plot_pred_ground(test_preds.numpy().ravel(), test_labels.numpy())

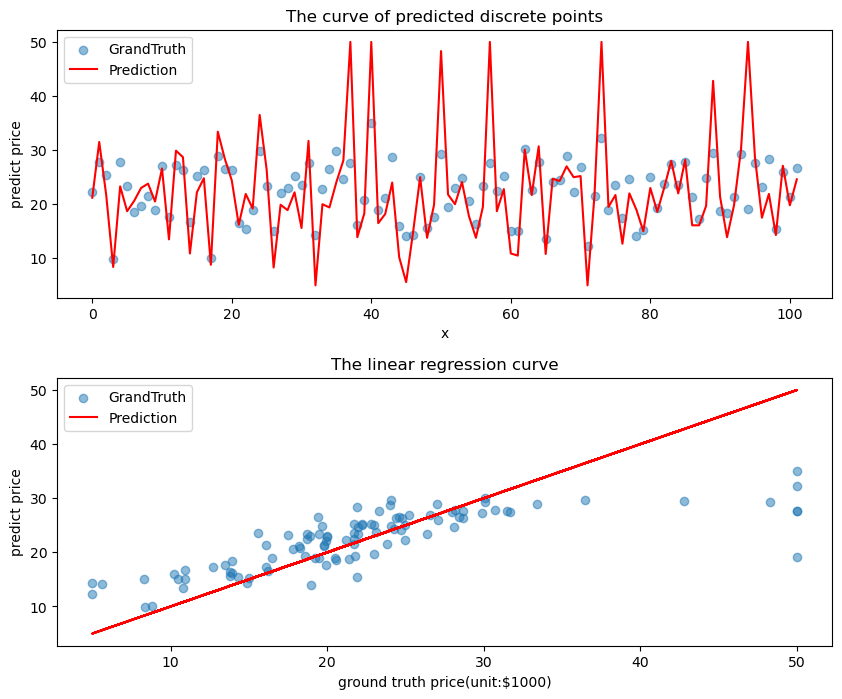
上图可以看出，训练出来的模型的预测结果与真实结果是较为接近的。

【项目006】基于线性回归的波士顿房价预测 隐藏答案 | 返回首页

【实验说明】

一、实验目的

二、实验要求

三、思维导图

四、目录结构

【实验一】环境配置

【实验二】数据集载入和预处理

2.0 Seaborn 库的安装

2.1 数据集介绍

2.2 数据集载入

2.3 数据分析及归一化处理

2.3.1 列表分析：使用pandas库将数据进行可视化

2.3.2 可视化分析

2.3.3 相关性分析

2.3.4 数据归一化处理

2.4 数据划分

【实验三】模型定义及训练

3.1 模型定义

3.2 定义训练过程的损失值可视化函数

3.3 模型训练

3.4 调用可视化函数显示训练损失曲线

【实验四】 模型的推理和预测

【项目006】基于线性回归的波士顿房价预测隐藏答案 | 返回首页

【实验四】模型的推理和预测