【项目005】初识神经网络:基于LeNet的Mnist手写数字识别(教学版) 隐藏答案 | 返回首页
作者:欧新宇(Xinyu OU)
当前版本:Release v1.1
开发平台:Paddle 2.5.2
运行环境:Intel Core i7-7700K CPU 4.2GHz, nVidia GeForce GTX 1080 Ti
本教案所涉及的数据集仅用于教学和交流使用,请勿用作商用。
最后更新:2022年9月17日
Mnist手写数字识别数据集是一个包含大量手写数字图片的公开数据集,常被用作计算机视觉和机器学习领域的基准测试。而LeNet作为早期卷积神经网络(Convolutional Neural Network, CNN)的代表之一,其结构简单且性能优越,是初学者理解CNN工作原理的理想模型。在本项目中,我们将从数据预处理开始,详细介绍Mnist数据集的加载、标准化和划分(训练集、验证集和测试集)。随后,我们将构建基于LeNet的神经网络模型,包括卷积层、池化层、全连接层以及激活函数等关键组件。在模型训练阶段,我们将使用适当的优化算法(如梯度下降)和损失函数(如交叉熵损失)来指导模型参数的更新,以最小化预测误差。最后,我们将对训练好的模型进行评估,并在测试集上验证其性能。通过本项目,读者将能够掌握神经网络的基本构建原理、训练过程以及评估方法。同时,通过实际操作,读者将能够加深对神经网络在图像识别领域应用的理解,为后续更复杂的计算机视觉任务打下坚实的基础。
【实验目的】
- 初步了解神经网络训练的基本过程和步骤;
- 学会使用Padlle内置库实现数据的载入、模型的载入;
- 学会Paddle的高阶API实现模型的训练、验证和推理;
- 学会如何利用训练好的模型对自定义提供的样本进行推理和预测。
- 本项目包含一个拓展练习,利用手写数字识别模型实现多个连续数字的识别,有兴趣的同学可以尝试一下。本项目只给出一种最简单(但并不通用)的字符切割方法。
【实验要求】
- 重点理解模型训练和推理的全流程和步骤;
- 使用MNIST的训练集进行模型训练,并使用测试集进行模型的评估和预测;
- 能够分别实现从测试集上获取样本和从硬盘上获取第三方的样本来进行预测;
【思维导图】
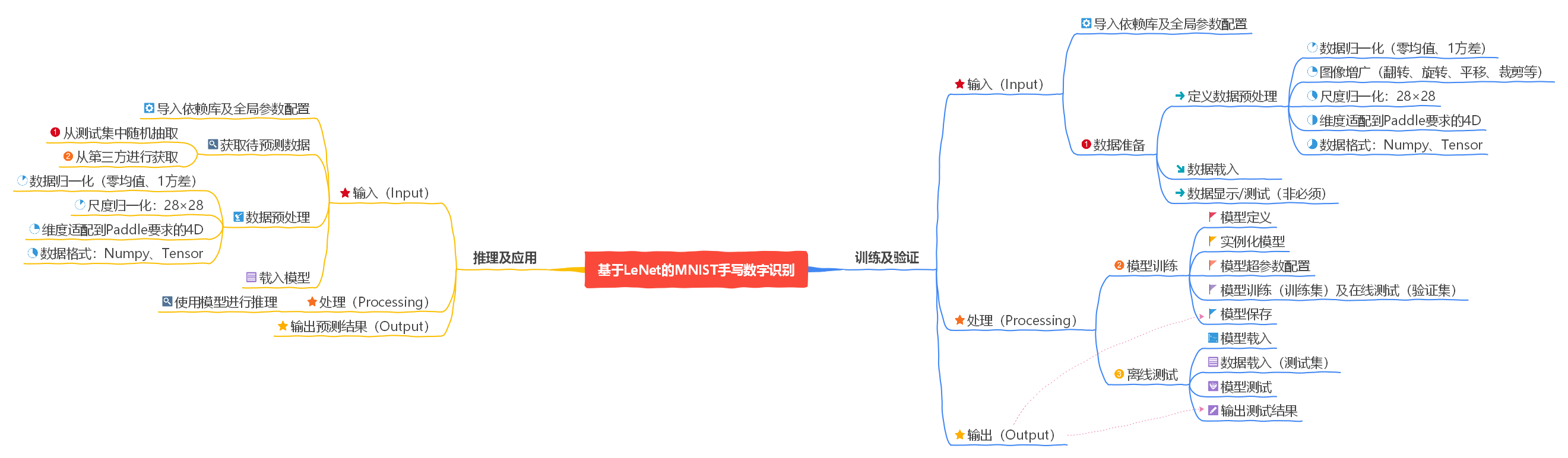
【目录结构】
- 本项目目录结构说明(可根据实际情况进行修改)
- 根目录:D:\Workspace\DeepLearning\WebsiteV2
- 项目默认目录:D:\Workspace\DeepLearning\WebsiteV2\Data\Projects\Project005LeNetMnist
- 图像资源目录:D:\Workspace\DeepLearning\WebsiteV2\Data\Projects\Project005LeNetMnist\Images
- 结果保存目录:D:\Workspace\DeepLearning\WebsiteV2\Data\Projects\Project005LeNetMnist
- 最终模型名称:final_model.pdparams, final_model.pdopt
【实验一】数据准备
实验难度:简单
实验摘要:使用Paddle内置工具包实现MNIST数据集的下载,并且对下载好的数据集进行可视化分析
实验目标:
- 学会使用paddle.vision.datasets库实现MNIST等常用数据集的下载,并且学会区分训练集和测试集合;
- 初步学会通过paddle.vision.transforms库实现数据集的预处理定义;
- 能够编写Python代码,从将读取出来的数据集中选择部分样本进行可视化分析。
实验建议:
- Paddle内置了transform图像预处理模块,包括反转、裁剪、亮度调节等图像增广操作,也能够是先零均值的图像归一化。在本项目中我们只实现图像归一化,其他数据增强技术我们将在后续的彩色图像分类中进行介绍。
- 本项目使用手写数字识别数据集MNIST进行实验,该数据集由28×28的灰度图组成,有兴趣的同学可以尝试使用Cifar10/100,FashionMNIST等彩色图像。
1.1 数据集简介
MNIST手写数字识别是深度学习的Hello World,它可以用来实现对0-9的10个类别的手写数字进行分类。该任务的配套数据集包含60000张训练图片和10000张测试图片,每个图片都对应于0-9中的一个数字,图片的分辨率是28×28的像素矩阵。下面给出部分图像的示例。

1.2 导入全局依赖及全局参数配置
import os
import cv2
import numpy as np
import matplotlib.pyplot as plt
import paddle
paddle.disable_static()
1.3 数据准备
1.3.1 定义数据预处理
数据预处理是深度学习工程应用中非常重要的一个环节,在计算机视觉任务中,它通过对图像样本进行多种变换可以实现训练样本规模和多样性的同时提升,从而提高模型的泛化能力。在paddle.vision.transforms中,飞桨也内置了如翻转、裁剪、调节亮度、去均值和方差等操作。在本任务中,我们会在初始化MNIST时,通过tansform字段实现Normalize变化的传入,Normalize实现就是零均值,1方差的图像归一化。图像归一化可以有效加快模型训练的收敛速度。
import paddle.vision.transforms as T
transform = T.Compose([T.Normalize(mean=[127.5], std=[127.5], data_format='CHW')])
1.3.2 数据载入
在paddle.vision.datasets库中,Paddle内置了若干常见的计算机视觉数据集,包括MNIST, Cifar10, Cifar100, FashionMNIST, Pascal VOC2012等。在本项目中,我们可以通过这个内置库实现MNIST数据集的加载。其中,训练集mode='train'用于训练模型,测试集mode='test'用于评估模型,这也是数据集最常见的使用方法之一。不过,这里的之一深有意味,我们后面会详细介绍在实际工程中,我们最好能将数据集划分训练集、验证集和测试集三个部分;而非仅仅只是训练集和测试集两部分。
# 从paddle.vision载入内置Mnist库,并使用transform类进行归一化预处理
train_dataset = paddle.vision.datasets.MNIST(mode='train', transform=transform)
test_dataset = paddle.vision.datasets.MNIST(mode='test', transform=transform)
print('数据载入完毕!')
数据载入完毕!
1.3.3 数据显示/测试
该步骤是非必须的必要步骤。非必须指它并不是训练和展示数据所必须的步骤;必要步骤是因为观察数据集有利于我们更好地理解数据,并选择合适的方法进行数据预处理。
# Q3:样本测试
# 1. 显示训练集和测试集的样本数
# 2. 随机(或指定)一个id,并从训练集中读取该ID的样本,并进行可视化观察,注意Mnist是灰度图
id = 5
data, label = train_dataset[id][0],train_dataset[id][1]
data = data.reshape([28,28])
plt.figure(figsize=(3,3))
plt.imshow(data, cmap='gray') # plt.cm.binary
print('训练集:{}张;测试集:{}张。\n 其中,第{}张测试图片的标签为:{}'.format(len(train_dataset), len(test_dataset), id, label))
训练集:60000张;测试集:10000张。
其中,第5张测试图片的标签为:[2]
【实验二】模型训练
实验难度:中等
实验摘要:使用Paddle内置工具包实现MNIST数据集的下载,并且对下载好的数据集进行可视化分析
实验目标:
- 理解训练集、验证集和测试集在模型训练中的作用;
- 初步学会通过
paddle.models库实现基本模型的载入和定义; - 能够使用
paddle.summary()方法实现模型结构的可视化,并初步理解各部分的含义; - 基本理解在线测试和离线测试的区别,并且能够使用Paddle高阶API实现模型的训练和验证;
- 学会使用
model.save()方法将训练好的模型进行保存。
实验建议:
- 重点理清模型训练的的基本流程,包括模型定义、模型实例化、模型超参数配置、模型训练和验证、模型测试。在本项目中每个部分的代码都比较简单,但在后续的任务中,我们将会进一步对各部分进行细化和自定义,因此此时理清整个结构对于后续的学习帮助较大。
- 模型的保存包括两种模式,一种仅用于推理,另一种可以同时用于恢复训练和推理。
2.1 配置网络
Paddle模型的网络配置一般包含三种方式,一是使用Paddle内置的模型,二是自定义组网,三是通过迁移学习直接载入预训练模型。在本项目中,我们使用Paddle内置的模型LeNet。
2.1.1 网络结构的定义
LeNet5是一个包含三个卷积层、两个最大池化层和两个全连接层的简单卷积神经网络,基本接入如下图所示

2.1.2 定义和实例化网络类
在使用Paddle内置模型进行模型设置时,我们只需要使用 paddle.vision.modles 库就可以了,它内置了包括AlexNet,VGG,ResNet,MobileNet,DenseNet等诸多经典模型。在该模型库中,我们可以通过 num_classes 字段来定义任务的类别数。此处,我们设置 num_classes=10 来实现0-9这10个数字的分类。
# 1. 初始化模型
LeNet = paddle.vision.models.LeNet(num_classes=10)
# 2. 可视化模型的配置信息
display(LeNet)
LeNet(
(features): Sequential(
(0): Conv2D(1, 6, kernel_size=[3, 3], padding=1, data_format=NCHW)
(1): ReLU()
(2): MaxPool2D(kernel_size=2, stride=2, padding=0)
(3): Conv2D(6, 16, kernel_size=[5, 5], data_format=NCHW)
(4): ReLU()
(5): MaxPool2D(kernel_size=2, stride=2, padding=0)
)
(fc): Sequential(
(0): Linear(in_features=400, out_features=120, dtype=float32)
(1): Linear(in_features=120, out_features=84, dtype=float32)
(2): Linear(in_features=84, out_features=10, dtype=float32)
)
)
2.1.3 测试模型并输出各层参数
# 1. 可视化模型的结构和参数
paddle.summary(LeNet, (1,1,28,28))
# 2. 模型测试
Xin = paddle.rand([3, 1, 28, 28]) # 生成随机数,形态为[NCHW]
Xout = LeNet(Xin) # 执行前向传输产生输出
print('输出的形态为:{}'.format(Xout.shape)) # 输出结果形态
---------------------------------------------------------------------------
Layer (type) Input Shape Output Shape Param #
===========================================================================
Conv2D-1 [[1, 1, 28, 28]] [1, 6, 28, 28] 60
ReLU-1 [[1, 6, 28, 28]] [1, 6, 28, 28] 0
MaxPool2D-1 [[1, 6, 28, 28]] [1, 6, 14, 14] 0
Conv2D-2 [[1, 6, 14, 14]] [1, 16, 10, 10] 2,416
ReLU-2 [[1, 16, 10, 10]] [1, 16, 10, 10] 0
MaxPool2D-2 [[1, 16, 10, 10]] [1, 16, 5, 5] 0
Linear-1 [[1, 400]] [1, 120] 48,120
Linear-2 [[1, 120]] [1, 84] 10,164
Linear-3 [[1, 84]] [1, 10] 850
===========================================================================
Total params: 61,610
Trainable params: 61,610
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.11
Params size (MB): 0.24
Estimated Total Size (MB): 0.35
---------------------------------------------------------------------------
输出的形态为:[3, 10]
2.2 定义过程可视化函数
2.3 模型训练与评估
从Paddle2.0开始,Paddle提供了不少快捷的模型配置和训练方法。基本的训练步骤主要可以分为以下几步:
- 模型封装。 使用paddle.Model实现模型封装,将网络组合成可以供高层API进行训练、评估、推理的实例。
- 模型配置。 使用paddle.Model.prepare完成模型训练的配置准备,包括定义优化器(paddle.optimzer)、损失函数(paddle.nn.Loss)和评价指标(paddle.metric)。
- 模型训练及在线测试。 使用paddel.Model.fit进行高层API训练,或编写自定义训练代码。本例将使用内置的高层API函数fit()进行训练,但后续的任务中我们更多的将使用自定义训练代码,因为自定训练代码便于我们植入符合需求的训练可视化、保存策略以及提示信息。在训练过程中,我们一般会同时使用一个验证集来实现模型的定期测试,以便我们在合适的时候调整训练进程和超参数。
- 离线测试。 使用paddle.Model.evaluate来实现对模型的评估,从严格意义上来说,模型评估应该使用测试集来说对模型进行评估,并且会从硬盘上读取训练中已经保存的checkpoint模型或final模型来进行评估。
2.3.1 配置训练基本参数
在本例中,我们将使用最常见的交叉熵损失来进行分类,并使用Adam优化算法和Accuracy精度指标来对模型进行评价。
# 1. 实例化模型
model = paddle.Model(LeNet)
# 2. 配置模型训练参数
model.prepare(
paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters()), # 优化函数Adam
paddle.nn.CrossEntropyLoss(), # 交叉熵损失函数
paddle.metric.Accuracy() # 精度评价指标
)
2.3.2 模型训练及在线测试
在训练过程中,主要超参数包括指定训练用的数据源train_dataset、验证用数据源test_dataset、训练论述epochs、训练的批大小batch_size。超参数verbose用于控制训练过程中是否显示日志。
# 训练模型
# device = paddle.set_device('gpu') # =cpu|gpu,程序通常会根据硬件情况,进行自动选择
model.fit(train_dataset, # 训练集
# test_dataset, # 测试集,设置后则在每个周期后进行验证,若不指定则不在验证集上进行验证
epochs=5, # 训练周期数
batch_size=64, # 训练的批次大小
verbose=1) # 是否显示训练日志
The loss value printed in the log is the current step, and the metric is the average value of previous steps.
Epoch 1/5
step 10/938 [..............................] - loss: 2.1836 - acc: 0.1328 - ETA: 21s - 23ms/step
step 938/938 [==============================] - loss: 0.0501 - acc: 0.9253 - 11ms/step
Epoch 2/5
step 938/938 [==============================] - loss: 0.0487 - acc: 0.9736 - 11ms/step
Epoch 3/5
step 938/938 [==============================] - loss: 0.0150 - acc: 0.9803 - 11ms/step
Epoch 4/5
step 938/938 [==============================] - loss: 0.0028 - acc: 0.9823 - 11ms/step
Epoch 5/5
step 938/938 [==============================] - loss: 0.0061 - acc: 0.9844 - 11ms/step
从训练过程的打印日志中,可观察到损失函数值 loss 逐渐变小,精度 acc 逐渐上升的趋势,反映出不错的训练效果。在后面的项目中,我们将设计一个绘图函数用于可视化训练过程的各种结果。
2.3.3 模型保存
将模型保存到硬盘后,再下一次使用模型进行预测时,就无需再进行训练,可以直接进行使用。模型的保存一般分为两种,第一种,仅用于推理使用,保存的模型只包含前向传输时所设计的参数,此时超参数 training=False;另一种模式的保存,还包含模型训练的优化器的参数,可以用于后续的恢复训练,此时超参数 training=True。
# 1. 定义根目录
# root_path = 'D://Workspace//DeepLearning//Websitev2' # Windows
root_path = '/home/aistudio' # AI Studio
# 2. 定义项目目录
# projcet_path = os.path.join(root_path, 'Data', 'Projects', 'Project005LeNetMNIST') # Windows
projcet_path = os.path.join(root_path, 'work') # AI Studio
# 3. 模型保存
model.save(os.path.join(projcet_path, 'final_model'), training=True)
2.4 离线测试
离线测试与在线测试最主要的区别是离线测试使用的是测试数据集 test_dataset,而在线测试一般使用的是验证数据集 eval_dataset。所以,我们会在训练时将训练好的模型保存到硬盘上,然后再通过 model.load() 命令重新将数据集进行载入并在测试数据集上进行验证。(当然,直接在训练好的模型上进行测试也可以)模型的离线测试可以调用 paddle.Model.evaluate 库实现评估评估完成后将输出模型在测试集上的损失函数值 loss 和精度 acc。
# 1. 载入模型
model.load(os.path.join(projcet_path, 'final_model'))
# 2. 运行评估函数在测试集上进行性能评估
model.evaluate(test_dataset, batch_size=64, verbose=1)
Eval begin...
step 157/157 [==============================] - loss: 9.3060e-05 - acc: 0.9815 - 8ms/step
Eval samples: 10000
{'loss': [9.3059774e-05], 'acc': 0.9815}
从结果可以看到,初步训练得到的模型精度在98%附近,在逐渐熟悉深度学习模型开发和训练技巧后,可以通过调整其中的训练参数来进一步提升模型的精度。
【实验三】 模型评估与推理(应用)
实验难度:中等
实验摘要:使用经过训练后保存的Paddle模型来完成对给定数据的推理与预测。
实验目标:
- 学会载入已训练好的模型;
- 学会获取测试集中的样本以从第三方收集获得的样本;
- 能够按照训练的规范对载入的数据进行预处理;
- 学会使用paddle.Model.predict()方法实现对预处理后的图像进行预测;
- 学会将预测结果进行输出。
实验建议:
- 按照给出的教案重点理清模型预测的基本流程,具体包括导入依赖库和全局参数配置、获取预测数据、对预测数据进行初始化、载入模型并进行预测、输出预测结果;
- 模型对数据进行预测时,要求数据具有完全相同的输入模式。这就意味着对于训练数据、验证数据和测试数据来说,需要使用相同的尺度、相同的图像归一化方法。因此,在进行推理的时候应该注意使用一致的预处理方法。此处,我们统一将模型压缩到
28×28,并且统一使用图像归一化将所有图像的均值置为0,方差置为1。
3.1 导入依赖库及全局参数配置
import os
import numpy as np
import cv2
import random
import matplotlib.pyplot as plt
import paddle
import paddle.vision.transforms as T
# 1. 定义根目录
# root_path = 'D://Workspace//DeepLearning//Websitev2' # Windows
root_path = '/home/aistudio' # AI Studio
# 2. 定义项目目录
# projcet_path = os.path.join(root_path, 'Data', 'Projects', 'Project005LeNetMNIST') # windows
projcet_path = os.path.join(root_path, 'work') # AI Studio
3.2 获取待预测数据
在本项目中我们将使用两种输入数据进行测试,一种是从给定的测试数据集中随机选择一幅图像进行测试,另一种是从硬盘上读取一张图像来进行测试。对于所有载入的图像都需要做一些预处理,主要包括以下几个方面:
- 将所有样本都resize到同样的尺度,例如本例的[28×28].
- 将图像数据转换为
numpy.array格式, 32bit浮点数据类型(float32) - 调整图像的通道为 (C,H,W)->(2,0,1), 原始图像通道为:(Height,Width,Channel)->(0,1,2)
- 将所有图像封装成[NCHW]的4D形态
transform = T.Compose([T.Normalize(mean=[127.5], std=[127.5])]) # 将数据归一化到[0~1]之间,也可以归一化为[-1,1]之间, img = img/255.0*2.0-1.0
TestMode = 'test_dataset' # test_dataset:测试集|Images:硬盘上的单独数据
if TestMode == 'test_dataset':
id = random.randrange(0,10000,1)
test_dataset = paddle.vision.datasets.MNIST(mode='test', transform=transform)
data, label = test_dataset[id][0],test_dataset[id][1]
data = data.reshape([28,28]) # resize image with high-quality 图像大小为28*28
img = data.reshape([1,1,28,28]).astype('float32')
print('第{}个测试数据的标签为:{}'.format(id, label))
elif TestMode == 'Images':
img_path = 'D:\\WorkSpace\\DeepLearning\\Website\\Data\\Projects\\Project004LeNetMNIST\\Images\\Single6.png'
data = cv2.imread(img_path, 0) # cv2.imread(path, 0|1),其中0表示灰度模式,1表示彩色模式
data = cv2.resize(data, (28, 28)) # resize image with high-quality 图像大小为28*28
img = np.array(data).reshape(1,1,28,28).astype('float32') # 返回新形状的数组,把它变成一个 numpy 数组以匹配数据馈送格式。 # cv2.imread(path, 0|1),其中0表示灰度模式,1表示彩色模式
# img = img/255.0
img = transform(img)
plt.figure(figsize=(3,3))
plt.imshow(data, cmap='gray') # plt.cm.binary
第8503个测试数据的标签为:[9]
<matplotlib.image.AxesImage at 0x255cfbfbbe0>
3.3 载入模型并开始进行预测
# 1.模型载入
LeNet = paddle.vision.models.LeNet(num_classes=10) # 初始化LeNet模型
model = paddle.Model(LeNet) # 用Model封装模型,并进行实例化
model.prepare() # 配置模型推理参数,此处无需设置额外参数,包括优化器,损失函数等
model.load(os.path.join(projcet_path, 'final_model'))
# 2.使用预先训练好的模型进行推理和预测
img = paddle.to_tensor(img) # 将numpy矩阵转换为paddle tensor
imgIn = paddle.unsqueeze(img, axis=0) # 将tensor扩展为5D形态,以适配paddle的输入要求
prob = model.predict(imgIn, verbose=0) # 使用model.predict()接口进行推理
pred = prob[0][0].argmax() # 输出推理结果中最大概率的标签
print('预测结果为:{}'.format(pred)) # 打印预测结果
预测结果为:9
【实验四】 拓展练习:使用LeNet对多个连续的数字进行识别(应用)
实验目的:学会用一些现有单独知识做一些拓展练习,特别是对接一些能落地的项目
实验建议:手写数字识别对输入样本有一定的要求,有兴趣的同学可以进行多种尝试,如何生成样本,如果对任意样本进行预处理等。
import os
import cv2
import numpy as np
import matplotlib.pyplot as plt
import random
import paddle
import paddle.vision.transforms as T
#########################全局参数定义#########################
# 1. 定义根目录
# root_path = 'D://Workspace//DeepLearning//Websitev2' # Windows
root_path = '/home/aistudio' # AI Studio
# 2. 定义项目目录
# projcet_path = os.path.join(root_path, 'Data', 'Projects', 'Project005LeNetMNIST') # Windows
projcet_path = os.path.join(root_path, 'work') # AI Studio
#########################模型训练#########################
# 1. 数据准备
# 1.1 定义数据预处理
transform = T.Compose([T.Normalize(mean=[127.5], std=[127.5], data_format='CHW')])
img_path = os.path.join(projcet_path, 'Images', 'Multi00.png')
data = cv2.imread(img_path, 0)
plt.imshow(data, cmap='binary')
# 3.模型载入和超参数配置
LeNet = paddle.vision.models.LeNet(num_classes=10) # 初始化LeNet模型
model = paddle.Model(LeNet) # 用Model封装模型,并进行实例化
model.prepare() # 配置模型推理参数,此处无需设置额外参数,包括优化器,损失函数等
model.load(os.path.join(projcet_path, 'final_model'))
result = []
for i in range(0,6):
x = data[:, i*150:(i+1)*150]
img = cv2.resize(x, (28, 28)) # resize image with high-quality 图像大小为28*28
img = np.array(img).reshape(1,1,28,28).astype('float32') # 返回新形状的数组,把它变成一个 numpy 数组以匹配数据馈送格式。 # cv2.imread(path, 0|1),其中0表示灰度模式,1表示彩色模式
img = transform(img)
img = paddle.to_tensor(img) # 将numpy矩阵转换为paddle tensor
imgIn = paddle.unsqueeze(img, axis=0) # 将tensor扩展为5D形态,以适配paddle的输入要求
prob = model.predict(imgIn, verbose=0) # 使用model.predict()接口进行推理
pred = prob[0][0].argmax() # 输出推理结果中最大概率的标签
result.append(pred)
print('预测结果为: {}'.format(result)) # 打印预测结果
预测结果为: [4, 1, 8, 7, 6, 3]

